Enunciado
Probabilidade e Estatística - Estatistica Mauri Guerra estatistica indutiva- Ed: 1º - Capítulo 14.Exercícios propostos - Ex. 1b
Num certo ano, foi feito um levantamento numa empresa, mês a mês, a respeito do custo total de fabricação por unidade produzida (), em cruzeiros, em função do gasto com matéria-prima (), em mil cruzeiros, e do número de funcionários (). Efetuando os cálculos dos somatórios necessários ao cálculo da regressão, obtivemos:
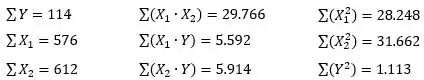
Pede-se:
- Calcular o coeficiente de explicação dessa regressão simples.
Passo 1
Olá galerinha, tudo bem com vocês? Vem comigo!
A regressão linear múltipla é a regressão em que sabemos como variáveis contribuem para a realização do fenômeno, e a parte funcional da regressão é uma função linear. Onde a estimativa da equação de regressão é dada por:
Onde as estimativas , , , , dos coeficientes , , , , podem ser calculadas pelo método dos mínimos quadrados, partindo de hipóteses análogas aquelas adotadas pela regressão linear simples.
Para o cálculo do coeficiente de explicação, para duas variáveis explicativas temos a seguinte equação:
Como no enunciado queremos o coeficiente de explicação da regressão linear simples de em função de , a equação fica:
Passo 2
Então vamos lá para nosso exercício. Pelo enunciado, conseguimos identificar que o levantamento da empresa foi feito mês a mês, durante um ano, ou seja:
Primeiramente, precisamos calcular a covariância entre e :
A variância de :
A covariância entre e :
E a variância de :
Passo 3
O cálculo de é dada pela seguinte equação:
Mas como queremos apenas para em função de :
Então conseguimos calcular o coeficiente de explicação da regressão simples para em função de :
Tchau galerinha, até mais!
Resposta
.