Enunciado
Probabilidade e Estatística - Walpole - Probabilidade e Estatística para Engenharia e Ciências- Ed: 8º - Capítulo 11.Exercícios - Ex. 4
Em certo tipo de teste em um espécime de metal, o estresse normal no espécime é conhecido como sendo funcionalmente relacionado com a resistência ao corte. A seguir temos um conjunto de dados experimentais sobre as duas variáveis:
(a) Estime a reta de regressão
(b) Estime a resistência ao corte para um estresse normal de 24,5 quilogramas por centímetro quadrado.
Passo 1
Selvaaaaaaaaaa galerinha, isso mesmo selva haha, tudo certinho??
“Hulk esmaga”, Bora esmagar essa questãozinha comigo?
Sabe se que, em um determinado tipo de corpo de prova de metal, a tensão normal em um corpo de prova está funcionalmente relacionada à resistência ao cisalhamento
- A curva de regressão necessária é , onde são os estimadores de a respectivamente, e são dados a seguir:
Passo 2
Agora vamos encontrar a inclinação partindo dos dados que foi fornecido.
Portanto, da tabela
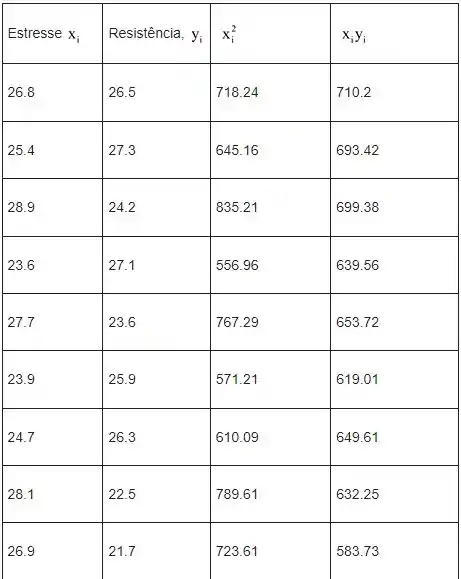
Passo 3
Vamos substituir os valores da tabela acima nas fórmulas dadas
Portanto, a curva de regressão ajustada é a seguinte
Passo 4
- A resistência ao cisalhamento estimada para uma tensão normal de 24.5 quilogramas por centímetro quadrado é de
“OK, isso foi legal.”
Resposta
Resposta nos passos.