Enunciado
Probabilidade e Estatística - Walpole - Probabilidade e Estatística para Engenharia e Ciências- Ed: 8º - Capítulo 11.Exercícios - Ex. 2
As notas de uma sala com nove estudantes em um relatório de meio de curso (x) e em um exame final (y) são as seguintes:
(a) Estime a reta de regressão linear.
(b) Estime a nota do exame final de um aluno que teve uma nota 85 no relatório de meio de curso.
Passo 1
E aí meus queridos? Tudo certinho?
“Operador! Me dê o número do responde ai!.... Preciso resolver essa questão”
Agora temos que estimar a linha de regressão linear para os dados fornecidos. Para os dados fornecidos, y é uma variável dependente (resposta) e x é independente (preditor). O cálculo é o seguinte:
A curva de regressão necessária é , onde são os estimadores de a respectivamente, e são dados a seguir:
Agora vamos encontrar a inclinação partindo dos dados que foi fornecido.
Portanto, da tabela
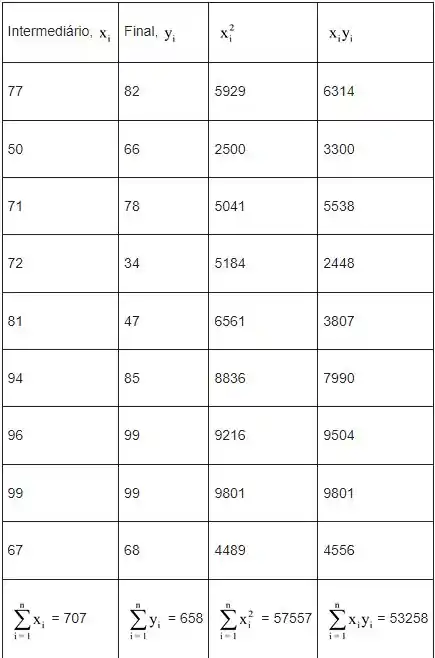
Passo 2
Vamos substituir os valores da tabela acima nas fórmulas dadas
Portanto, a curva de regressão ajustada é a seguinte
Passo 3
(b) A estimativa da nota do exame final de um aluno que obteve nota 85 no relatório intermediário é a seguinte:
Portanto, a estimativa do exame final é de
"Se algo é difícil de fazer, vale a pena ser feito!"
Resposta
Vide a explicação.