Enunciado
Probabilidade e Estatística - Walpole - Probabilidade e Estatística para Engenharia e Ciências- Ed: 8º - Capítulo 11.Exercícios - Ex. 3
Um estudo foi realizado sobre a quantidade de açúcar convertido em um processo em várias temperaturas. Os dados foram codificados e registrados a seguir:
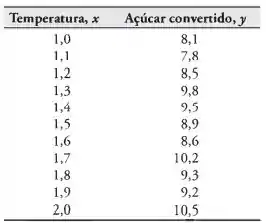
(a) Estime a reta de regressão linear.
(b) Estime a média da quantidade de açúcar convertido produzida quando a temperatura codificada é 1,75.
(c) Faça um gráfico dos resíduos versus a temperatura. Comente.
Passo 1
E ai seres de luz, tudo bem?
Como diz o Homer “Filho, este aparelhinho vai nos ajudar a escapar dessa fria!”
Aqui nos é dada a quantidade de açúcar convertido (x) em determinado processo em várias temperaturas (y).
- Agora temos que estimar a linha de regressão linear para os dados fornecidos. Para os dados fornecidos, y é a variável de resposta ex é a variável preditora.
- A quantidade média de açúcar convertido produzida quando a temperatura codificada dada é 1.75 e dada como mostra
- Vamos encontrar os resíduos, que são dados na tabela a seguir
A curva de regressão necessária é , onde são os estimadores de a respectivamente, e são dados a seguir:
Passo 2
Agora vamos encontrar a inclinação partindo dos dados que foi fornecido.
Portanto, da tabela
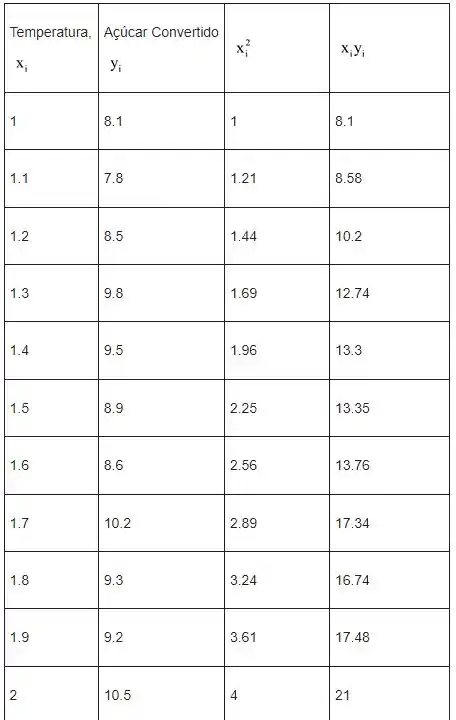
Passo 3
Vamos substituir os valores da tabela acima nas fórmulas dadas
Portanto, a curva de regressão ajustada é a seguinte
Passo 4
Passo 5
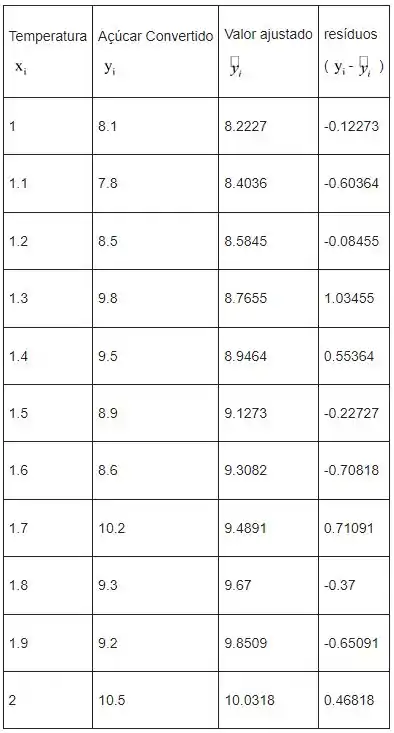
Passo 2
Logo abaixo temos o gráfico de dispersão para os resíduos versus os x´s (temperatura).
Vamos usar o MiniTab
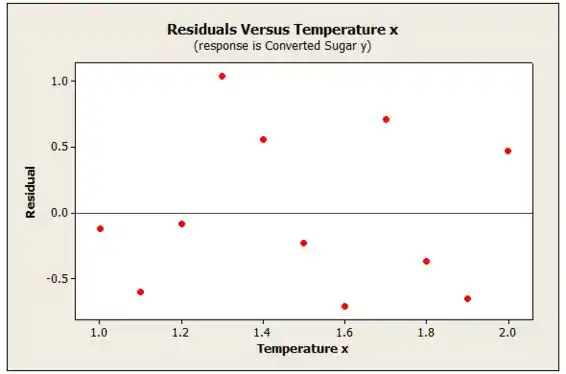
A partir do gráfico de dispersão podemos observar que há uma grande variação nos resíduos à medida que se afastam da linha central.
Aqui podemos observar que há aumento nos valores residuais à medida que a temperatura aumenta.
“Eu não estava mentindo! Estava escrevendo ficção com a boca.”
Resposta
Resposta nos passos