Cinco prêmios diferentes (melhor desempenho escolar, melhores qualidades de liderança, e assim por diante) serão dados a estudantes selecionados de uma classe de trinta alunos. Quantos resultados diferentes são possíveis se
(a) Um estudante puder receber qualquer número de prêmios?
(b) Cada estudante puder receber no máximo um prêmio?
Passo 1
Opa galeeeeera! Hoje vamos entender mais um pouco sobre o Princípio Fundamental da Contagem (PFC).
Vamos pensar que cada prêmio é uma colocação:
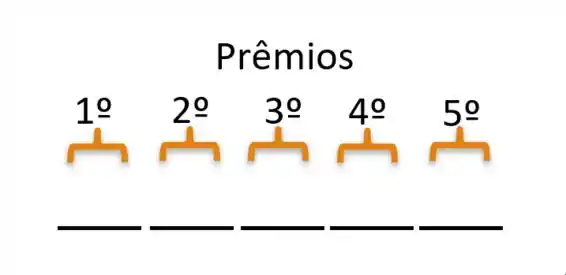 Vamos pensar quantas possibilidades temos para cada prêmio e utilizar o PFC para encontrar quantos resultados diferentes existem.
Vamos pensar quantas possibilidades temos para cada prêmio e utilizar o PFC para encontrar quantos resultados diferentes existem.
Passo 2
a) Como neste caso uma mesma pessoa pode receber todos os prêmios, a contagem fica simples. Qualquer estudante pode receber qualquer prêmio, como existem 30 alunos teremos 30 possibilidades para cada prêmio:
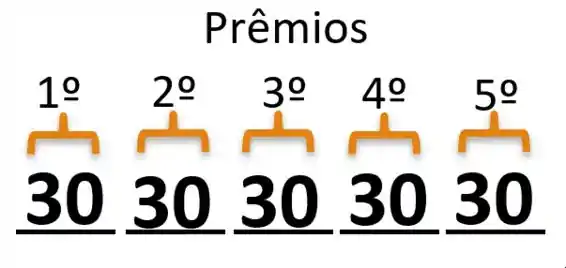
Passo 3
Acabamos de escolher o primeiro colocado e depois o segundo ... e depois o quinto colocado. Como o PFC diz, toda vez que aparecer um “e” no nosso argumento precisaremos multiplicar as possibilidades de cada colocado para achar a quantidade de formas possíveis. Assim:

Fazendo as contas diferentes possibilidades de dar estes 5 prêmios.
Passo 4
b) Agora cada pessoa pode receber no máximo um prêmio, vamos pensar como isto seria feito. Para o primeiro prêmio poderíamos escolher qualquer um dos 30 alunos, sendo então 30 possibilidades:
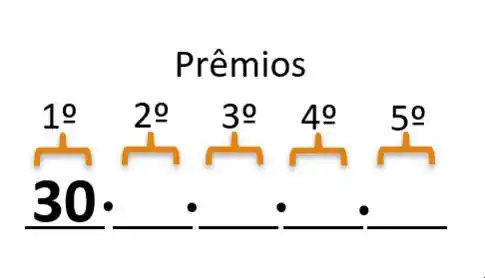
Como já escolhemos um ganhador e ele não pode ser escolhido novamente, só restaram 39 possibilidades para o segundo premio, então:
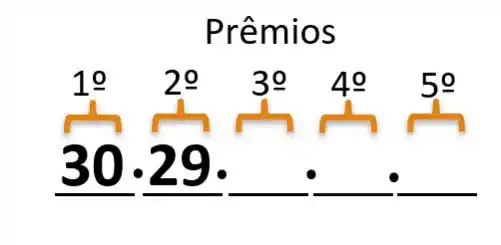
Passo 5
E analogamente cada possição a seguir terá uma possibilidade a menos, já que uma pessoa terá sido escolhida no premio anterior.
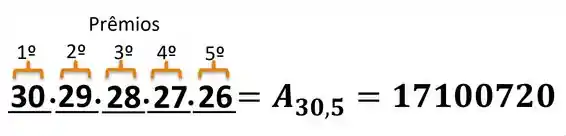
Note que todo esse raciocineo que fizemos se resume ao Arranjo de escolhe (), que nada mais é do que de quantas formas podemos escolher em ordem 5 pessoas dentre 30. E vimos que é possivel resolver essas questões sem utilizar formulas decoradas.
Resposta
a) 24300000 possibilidades
b) 17100720 possibilidades