Enunciado
Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 8.Problemas - Ex. 31f
Numa comunidade em que apenas dez casais trabalham, fez-se um levantamento no qual foram obtidos os seguintes valores para os rendimentos anuais:
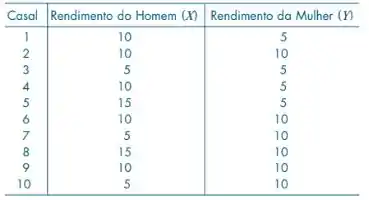
Um casal é escolhido ao acaso entre os dez. Seja X o rendimento do homem e Y o da mulher. Supondo que todos os casais tenham a renda de um ano disponível, e que se oferecerá ao casal escolhido a possibilidade de comprar uma casa pelo preço de 20, qual a probabilidade de que o casal escolhido possa efetuar a compra?
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para pegar o que aconteceu lá na combinação das variáveis e encontrar a probabilidade do evento. Parece muita coisa, mas é tranquilo. Partiu??
Passo 2
Ok, nosso primeiro passo vai ser montar a tabela de distribuição para .
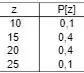
Agora, vamos analisar a distribuição.
Passo 3
Pela tabela, vemos que 0,4 dos casais consegue comprar pelo preço de 20 e 0,1 pelo preço de 25. Então, 0,5 dos casais está apto à compra com valor de 20.
Resposta
0,5 dos casais está apto à compra com valor de 20.