Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 1.Exercícios Suplementares - Ex. 78

Considere uma amostra x 1 , x 2 , … , x n e suponha que os valores de x - , s 2 e s tenham sido calculados. a. Assuma y i = x i - x - para i   =   1 , … , n . Como os valores de s² e s dos y i se comparam aos valores correspondentes dos x i ? Explique

Passo 1

Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊

  1. Do exercico 69 (a) nós provamos que

    2. y i = a x i + b

    Então nós temos que

    y -   =   a x - + b

    Nesse caso particular nós temos que

    y i = 1 ∙ x i + x -

    Onde a   =   1   ;   b   =   x -

    Também, dos mesmos exercícios (a) nós temos que

    s y 2 = a 2 s x 2

    O que no nosso caso

    s y 2 - a 2 ∙ s y 2 = 1 2 ∙ s y 2 = s x 2

    s y = a ∙ s y = 1 ∙ s y = s x

    ‎Então, já que subtraímos a constante ‎ x ¯ ‎ de cada um dos valores, o desvio padrão da amostra e a variância amostral não mudam.‎

    Passo 2

  2. Os números  z i ​ são conhecidos como os pontos de dados padronizados. Fazendo o mesmo que fizemos em (a) temos para

Então a e b são

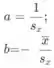
‎Usando isso, e exercício 69 (a) temos‎

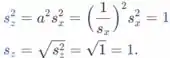
Passo 2

  1. São idênticos
  2. s z 2 = s z = 1

Resposta

Resposta nos passos

Exercícios de Livros Relacionados

Um Diagrama de Pareto é uma variação de um histograma para dados categorizados resultantes de um estudo de controle de qualidade. Cada categoria representa um tipo diferente de não-conformidade de pro
Uma amostra de n = 10 automóveis foi selecionada e cada um deles foi sujeito a um teste de colisão a 5 mph. Representando um carro sem danos visíveis por S (de sucesso) e um carro com danos por F, os
O artigo “Snow Cover and Temperature Relationships in North America and Eurasia” (J. Climate and Applied Meteorology, 1983, p. 460-469) usou técnicas estatísticas para relacionar a quantidade de cober
A pressão mínima de injeção (psi) em amostras de moldagem por injeção de milho de alta amilose foi determinada para oito amostras diferentes (pressões mais altas correspondem a maior dificuldade de pr
O Exercício 36 na Seção 1.3 apresentou uma amostra de 26 tempos de fuga dos trabalhadores de uma plataforma de petróleo em uma simulação de fuga. Calcule e interprete o desvio padrão amostral. (Dica: