Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Meyer - Aplicações a Estatística- Ed: 2º - Capítulo 11.Problemas - Ex. 20

Considere os componentes A ,   A ' ,   B ,   B '   e   C ligados de maneira indicada nas Figs. 11.12 (a) e (b). (O componente C pode ser considerado como uma “defesa”, quando ambas A e B deixarem de funcionar.) Represente as confiabilidades dos componentes isoladamente por R A ,   R A ' ,   R B ,   R B '   e   R C (e admitindo que os componentes funcionem independentemente um do outro).

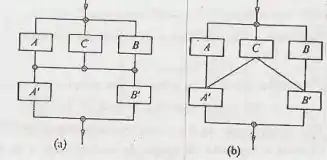
Admitido que todos os componentes incluídos tenham a mesma taxa de falhas constante λ , estabeleça a expressão da confiabilidade R(t) do sistema apresentado na Fig. 11.12(b). Determine, também, a duração até falhar média, desse sistema.

Passo 1

Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para encontrarmos o nosso valor esperado. Parece muita coisa, mas é tranquilo. Partiu??

Passo 2

Ok, nosso primeiro passo vai ser relembrar o que o exercício nos deu. Preparado??

R t = 1 - 1 - R 1 t 1 - R 2 t 1 - R 3 t

R S = P S = 1 - P S -

Com essa estrutura de probabilidade, podemos arrumar para botar em função do primeiro valor da distribuição dela. Lembra como faz?? Não?? Vai lá na teoria que eu te esperoaqui...

Achou?? Então me diz aii...

R t = 1 - F t = ∫ f s d s

R S t = 1 - 1 - R 1 t 1 - R 2 t … 1 - R n t

R S t = 1 - 1 - r t n

E T = ∫ R S d t

r t = e - λ t

Com isso, podemos começar a pensar.

R S = 1 - P S -

P S - = P T + P V - P T ∩ V

P T = 1 - R C 1 - R A R A ' 1 - R B R B '

P V = 1 - R A 1 - R B

P T ∩ V = 1 - R C 1 - R A 1 - R B

R S = 1 - 1 - R C 1 - R A R A ' 1 - R B R B ' - R C 1 - R A 1 - R B  

Passo 3

Pronto!! Agora é só obter nossa distribuição!!

R S = 1 - 1 - e - λ t 1 - e - 2 λ t 1 - e - 2 λ t - e - λ t 1 - e - λ t 1 - e - λ t

R S = e - 5 λ t - e - 4 λ t - 3 e - 3 λ t + 4 e - 2 λ t  

E T = 19 20 λ

Resposta

R S = e - 5 λ t - e - 4 λ t - 3 e - 3 λ t + 4 e - 2 λ t  

E T = 19 20 λ

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Suponha que a taxa de falhas, associada com a duração da vida T de uma peça, seja dada pela seguinte função Z t =C 0 ,0 ≤ t , t 0 C 0 + C 1 t - t 0 ,t ≥ t 0 Estabeleça a fdp de T, a duração até falhar
Suponha que cada um de três dispositivos eletrônicos tenha uma lei de falhas dada por uma distribuição exponencial, com parâmetros b1, b2 e b3, respectivamente. Suponha que esses três dispositivos fun
Um artigo na revista Naclear Engineering International Fevereire de 1988, p. 33) Testes Varias caracteristicas de bastées combustiveis usades em um reator pertencente a uma central de utilidade na Nor
Um artigo na revista Cancer Research "Analyses of limer-matehed time-to-response data, with modifications for recovery of interliacr in. formation" — Analises de dados de tempo de resposta para ninhad
Um artigo na revista Australian Journal of Agricultural Research. "Non-Starch Polysaccharides and Broiler Performance on Diets Comtaining Soyabean Meal as the Sole Protein Concentrare" - Polisxacaride