Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Walpole - Probabilidade e Estatística para Engenharia e Ciências- Ed: 8º - Capítulo 3.Exercícios - Ex. 67

Considere o número de ligações recebidas por uma central telefônica durante um intervalo de cinco minutos uma variável aleatória X com função de probabilidade

f x = e - 2 2 x x ! ,         p a r a   x = 0 ,   1 ,   2 …

(a) Determine a probabilidade de que X seja igual a 0, 1, 2, 3 ,4, 5 e 6.

(b) Faça um gráfico da função massa da probabilidade para esses valores de   X .

(c) Determine a função de distribuição acumulada para esses valores de X .

Passo 1

Falaa, meu querido/minha querida. Para encontramos a probabilidade de que X seja igual a algum valor de x , basta inserirmos os valores na equação dada pelo enunciado.

Agora, para encontrarmos a função de distribuição acumulada, temos a seguinte fórmula:

F x = ∑ y ≤ x f ( y )

Então, bora para os cálculos!!!

Passo 2

Como foi dito no Passo 1, basta substituirmos os valores pedidos pelo enunciado na fórmula:

P X = 0 = f 0 = e - 2 = 0,1353

P X = 1 = f 1 = 2 e - 2 = 0 , 2707

P X = 2 = f 2 = 2 e - 2 = 0 , 2707

P X = 3 = f 3 = 4 e - 2 3 = 0 , 1804

P X = 4 = f 4 = 2 e - 2 3 = 0 , 0902

P X = 5 = f 5 = 4 e - 2 15 = 0 , 0361

P X = 6 = f 6 = 4 e - 2 45 = 0 , 012

Passo 3

Usando os valores da letra (a) para construirmos o gráfico, temos:

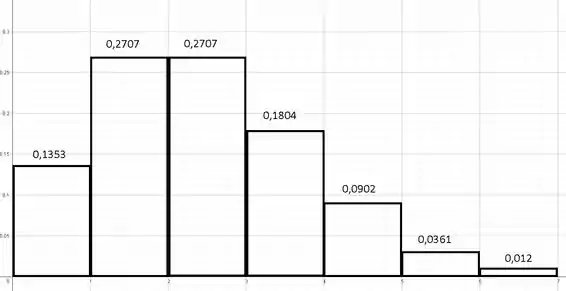
Passo 4

Como definirmos no Passo 1, a fórmula para encontrarmos a função de distribuição acumulada é:

F x = ∑ y ≤ x f ( y )

Sendo assim, temos:

F 0 = f 0 = 0,1353

F 1 = f 0 + f 1 = 0,406

F 2 = f 0 + f 1 + f 2 = 0,6767

F 3 = f 0 + f 1 + f 2 + f ( 3 ) = 0,8571

F 4 = f 0 + f 1 + f 2 + f 3 + f 4 = 0,9473

F 5 = f 0 + f 1 + f 2 + f 3 + f 4 + f ( 5 ) = 0,9834

F 6 = f 0 + f 1 + f 2 + f 3 + f 4 + f 5 + f ( 6 ) = 0,9954

Resposta

Resolução nos passos anteriores.

Exercícios de Livros Relacionados

Intervalos de classes desiguais. É muito comum o uso de classes com tamanhos desiguais no agrupamento dos dados em tabelas de freqüências. Nestes casos deve-se tomar alguns cuidados especiais quanto à
Em uma tarefa em um laboratório, se o equipamento estiver funcionando, a função densidade do resultado observado X , é f x = 2 1 - x , 0x1 0 , c a s oc o n t r á r i o á (a) Calcule P ( X ≤ 1 / 3 ) .(
Um processo industrial fabrica itens que podem ser classificados como defeituosos ou não defeituosos. A probabilidade de que um item seja defeituoso é de 0,1. Um experimento é conduzido, no qual cinco
Certo ponto-de-venda produz calças. As calças são checadas por um grupo de dez funcionários. Eles inspecionam calças retiradas aleatoriamente da linha de produção. Cada inspetor é designado por um núm