Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 13.Exercícios - Ex. 9
Considere os quatro conjuntos de dados a seguir; os três primeiros têm os mesmos valores , de modo que esses valores são relacionados apenas uma única vez (Frank Anscombe, "Graphs in Statistical Analysis", Amer Statistician, 1973, p. 17-21):
Para cada um desses quatro conjuntos de dados, os valores das estatísticas e são praticamente idênticos, de modo que todas as quantidades calculadas com base nesses cinco termos serão essencialmente idênticas para os quatro conjuntos - a reta dos mínimos quadrados , intervalos , estatísticas , e assim por diante. As estatísticas não apresentam nenhuma maneira de diferenciar os quatro conjuntos de dados. Com base no gráfico de dispersão e no gráfico dos resíduos de cada conjunto, fale sobre a aplicabilidade ou inadequação de ajustar um modelo de linha reta; inclua em seus comentários qualquer sugestão específica sobre como uma "análise de linha reta" deveria ser modificada ou qualificada
Passo 1
Tanto um gráfico de dispersão quanto um gráfico de resíduos (com base no modelo de regressão linear simples) para o primeiro conjunto de dados sugerem que um modelo de regressão linear simples é razoável, sem padrões ou pontos de dados influentes que indiquem que o modelo deve ser modificado. No entanto, gráficos de dispersão para os outros três conjuntos de dados revelam dificuldades.
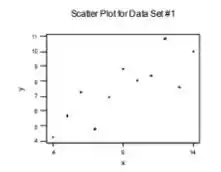
Para o conjunto de dados nº 2, uma função quadrática forneceria claramente um ajuste muito melhor. Para o conjunto de dados nº 3, a relação é perfeitamente linear, exceto um valor atípico, que obviamente influenciou muito o ajuste, embora seu valor x não seja incomumente grande ou pequeno. Os sinais dos resíduos aqui (correspondentes a x crescente) são ++++⋯+⋯ e um gráfico de resíduos refletiria esse padrão e sugeriria uma análise cuidadosa do modelo escolhido. Para o conjunto de dados int, fica claro que a inclinação da linha de mínimos quadrados foi determinada inteiramente pelo outlier, portanto, esse ponto é extremamente influente (e seu valor x está longe dos demais).
Resposta
Para o conjunto de dados int, fica claro que a inclinação da linha de mínimos quadrados foi determinada inteiramente pelo outlier, portanto, esse ponto é extremamente influente (e seu valor x está longe dos demais).