Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 13.Exercícios - Ex. 27
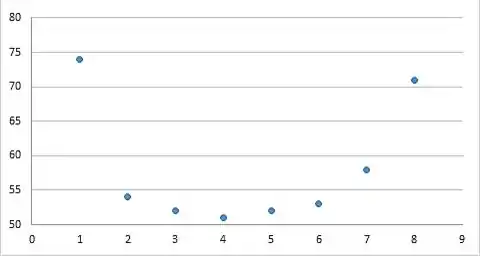
Os dados a seguir sobre y concentração de glucose (g/L) e x tempo de fermentação (dias) para uma determinada mistura de licor de malte foram reproduzidos de um gráfico do artigo “Improving Fermentation Productivity with Reverse Osmosis” (Food Tech., 1984, p. 92–96):
a. Verifique se o gráfico de dispersão dos dados é consistente com a escolha do modelo de regressão quadrática. b. A equação de regressão quadrática estimada é y 84,482 15,875x 1,7679x2 . Preveja o valor da concentração de glucose para um tempo de fermentação de 6 dias e calcule o resíduo correspondente. c. Usando SQE 61,77, que proporção da variação observada pode ser atribuída à relação de regressão quadrática? d. Os n 8 resíduos padronizados, baseados no modelo quadrático, são 1,91, 1,95, 0,25, 0,58, 0,90, 0,04, 0,66 e 0,20. Construa um gráfico dos resíduos padronizados versus x e um gráfico de probabilidade normal. Os gráficos exibem alguma característica indesejável? e. O desvio padrão estimado de ˆY6 — isto é, ˆ 0 ˆ 1(6) ˆ 2(36) — é 1,69. Calcule um IC de 95% para Y6. f. Calcule um IP de 95% para uma observação sobre concentração de glicose feita seis dias depois do tempo de fermentação.
Passo 1
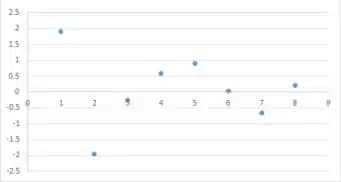
- O gráfico de dispersão sugere que a regressão quadrática pode ser apropriada
- A partir do modelo de regressão quadrática estimado, a previsão quando , é
- O coeficiente de determinação, r², é
- A tabela a seguir resume o valor necessário para calcular o gráfico de probabilidade normal
- Um intervalo de confiança de para a média de YY quando
- Intervalo de previsão
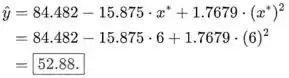
Os valores ajustados são valores obtidos substituindo na linha de regressão. Os residuais são a diferença entre os valores observados e ajustados.
O resíduo é
Passo 2
A soma total dos quadrados é
A soma total dos quadrados é
Assim, o coeficiente de determinação, ou a proporção de variação observada atribuída à regressão, é
Passo 3
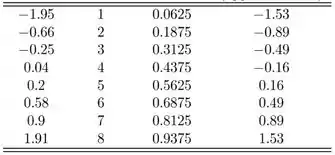
O gráfico de probabilidade normal sugere que os dados são normalmente distribuídos
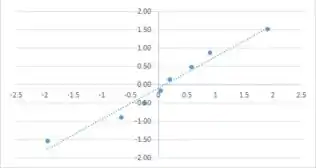
A partir do padronizado pode-se ver que não há outliers, e que nenhum dos resíduos excede dois em magnitude.
Onde
e onde é o desvio padrão estimado de .
Do exercício (b), quando , o valor ajustado é
e o desvio padrão estimado do valor ajustado (dado no exercício) é
A partir da tabela no apêndice pode-se encontrar o valor t
Um intervalo de confiança de para a média de Y quando é
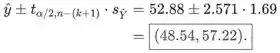
Onde
e onde é o desvio padrão estimado de é um intervalo de previsão de 100(1−α)% para uma observação futura Y, quando
Como acima, quando , o valor ajustado é
e o desvio padrão estimado do valor ajustado é
A partir da tabela no apêndice pode-se encontrar o valor t
A estimativa do desvio padrão σ é
assim, um intervalo de previsão de 99% para observação futura quando é
Resposta
Ver o desenvolvimento