Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 13.Exercícios - Ex. 26
Além da regressão linear da densidade real na quantidade de umidade, o artigo citado no Exercício 6 avaliou a regressão quadrática da densidade de massa versus quantidade de umidade. Os dados de um gráfico do artigo são apresentados a seguir, com o resultado do MINlTAB de aderência quadrática
a. Um gráfico de dispersão dos dados parece consistente com o modelo de regressão quadrática? b. Que proporção da variação observada na densidade pode ser atribuída à relação do modelo? c. O modelo quadrático parece útil? Execute um teste ao nível de significância 0,05. d. A última linha do resultado provém da solicitação de informações sobre estimativa e previsão quando uma quantidade de umidade é 14. Calcule um PI de 99% para a densidade quando a quantidade de umidade é 14. e. A previsão quadrática parece fornecer informações úteis? Teste as hipóteses apropriadas ao nível de significância 0,0
Passo 1
- Gráfico de dispersão
- A proporção de variação nas variáveis y explicada pelo modelo de regressão é dada pelo coeficiente de determinação.
O teor de umidade está no eixo horizontal e a densidade aparente está no eixo vertical.
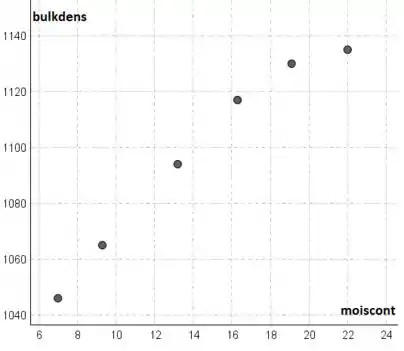
Observamos que o padrão no gráfico de dispersão parece ser aproximadamente uma parábola e, portanto, um modelo de regressão quadrática parece ser apropriado.
O coeficiente de determinação é dado à direita de "R-Sq" na saída do MINITAB:
Assim, 93.8% da variação observada na densidade pode ser atribuída à relação modal.
Passo 2
A hipótese nula afirma que todos os coeficientes são zero, enquanto a hipótese alternativa afirma o contrário.
O valor P correspondente ao teste F global é fornecido na linha "Regressão" e na coluna "P" da tabela de Análise de Variância na saída do Minitab:
Se o valor P for menor que o nível de significância, rejeite a hipótese nula
Há evidências suficientes para apoiar a afirmação de que pelo menos um dos coeficientes é diferente de zero e, portanto, o modelo quadrático parece ser útil.
O valor previsto para y é fornecido abaixo de "Ajustar" na última linha da saída do MINITAB:
O desvio padrão do ajuste é fornecido abaixo de "StDev Fit" na última linha da saída do MINITAB:
o desvio padrão da estimativa é dado à direita de S= da saída do MINITAB
Determine o valor t olhando na linha começando com graus de liberdade e na coluna com na tabela da distribuição T de Student no apêndice:
Os limites do intervalo de previsão são então:
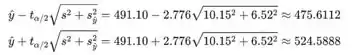
Estamos 99% confiantes de que a densidade está entre 475.6112 e 524.5888 quando o teor de umidade é 14.
Passo 3
Dada a afirmação: o termo quadrático do coeficiente é diferente de zero
A hipótese nula ou a hipótese alternativa afirma a afirmação dada A hipótese nula afirma que a inclinação é zero. Se a afirmação dada é a hipótese nula, então a hipótese alternativa afirma o oposto da hipótese nula.
O valor P do coeficiente do termo quadrático é dado na linha "constsqd" e na coluna "P" da saída do MINITAB:
Se o valor P for menor que o nível de significância, rejeite a hipótese nula
Há evidências suficientes para apoiar a afirmação de que o preditor quadrático parece fornecer informações úteis
Resposta
- Sim
- Sim
- Sim