Considere os três conjuntos de dados a seguir, nos quais as variáveis de interesse são x distância de comutação e y tempo de comutação. Com base em um gráfico de dispersão e nos valores de s e r2 , em que situação a regressão linear simples seria a mais (menos) eficaz e por quê?
Passo 1
Crie três gráficos de dispersão usando os dados fornecidos. Observando os gráficos de dispersão, você pode notar que, para os conjuntos de dados 2 e 3, a linha de regressão e os pontos de dados são bastante próximos e há uma forte relação linear entre as variáveis. No entanto, no conjunto de dados 1 a relação linear não é tão forte
#1
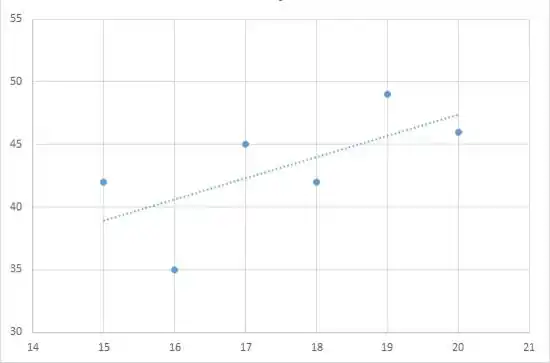
#2

Passo 2
#3
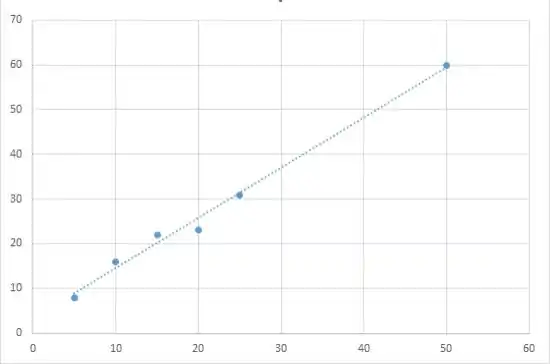
Passo 3
Para o conjunto de dados 1, a estimativa de variância é
e o coeficiente de determinação é
Para o conjunto de dados 2, a estimativa de variância é
e o coeficiente de determinação é
Para o conjunto de dados 3, a estimativa de variância é
e o coeficiente de determinação é
Quanto maior é, melhor. Além disso, quanto menor s, melhor. O maior está no conjunto de dados 2 e no conjunto de dados 3 que é igual a . No entanto, o menor ss está no conjunto de dados 3; assim o modelo de regressão linear simples mais eficaz seria para conjunto de dados 3. O menor e o maior ss é para o conjunto de dados 1; assim, o modelo de regressão linear simples menos eficaz seria para conjunto de dados 1.
Resposta
O mais eficaz - para o conjunto de dados 3;
O menos eficaz - para o conjunto de dados 1.