Estabeleça as hipóteses de interesse nesse experimento.

Teste as hipóteses anteriores e tire conclusões, usando a análise de variância com .

Analise os residuos desse experimento.

Beleza, considerando os dois fatores ( e ), onde é o total de observações feitas no nível do fator , é o total de observações feitas no nível do fator , É o total de observações na célula e é o total de todas as observações. Definindo correspondendo a linha, coluna, célula e média. Usamos para construir a tabela ANOVA as formulas:

; ; ;

Bom galera, para testar os efeitos do fator de linha são todos iguais a zero (), usando a razão , que tem uma distribuição com e com graus de liberdade. Para testar se o fator efeito da coluna são todos iguais a zero (), usando a razão , que tem uma distribuição com e graus de liberdade. E para testar que a interação de todos os efeitos são zero, usando a razão , que tem distribuição com e graus de liberdade.

Show de bola, Geralmente é melhor realizar o teste para interação 1os. e depois avaliar os principais efeitos. Se a interação não for significativa, A interpretação do teste sobre os principais efeitos é simples. Se a interação for significativa, os principais efeitos envolvidos na interação podem não ter muito valor interpretativo prático.

Fazemos o ANOVA no Minitab e temos como resultado:

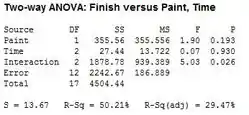
O valor do teste para interação é de , Como é inferior a , pode-se concluir que é no nível de a interação é significativa. Portanto, nenhuma conclusão sobre os principais efeitos pode ser feita utilizando-se a analise da variância. Mais testes devem ser realizados.

Por fim, para analisar melhor plotamos os gráficos de resíduos:

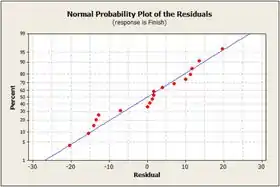
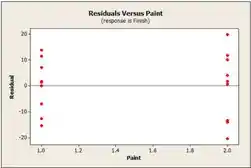
O gráfico de probabilidade normal não indicam qualquer desvio da normalidade. Os lotes de resíduos são bastante simétricos sobre , embora mostre valores um pouco mais positivos do que negativos.