Construam gráfico de probabilidade normal dos dados de alturas dos exercícios 6.22 e 6.29. Faça um gráfico para os dados de alunos e de alunos nos mesmos eixos. A altura parece ser normalmente distribuídas para ambos os grupos de estudantes? Se as duas populações têm a mesma variância, os dois gráficos de probabilidade normal devem ter as mesmas inclinações. Que conclusões você tiraria acerca das alturas dos dois grupos de estudantes, a partir do exame visual dos gráficos de probabilidade normal?
Passo 1
Para as mulheres:
Os valores dos dados estão no eixo horizontal e o padrão dos valores normais estão no eixo vertical.
Se os dados contiverem n valores de dados, então os valores normais padronizadas são os valores na tabela III correspondente a uma área de (ou a área mais próxima) com
O menor valor padronizado corresponde ao menor valor de dados, o segundo menor valor padronizado corresponde ao segundo menor valor de dados e assim por diante.
Passo 2
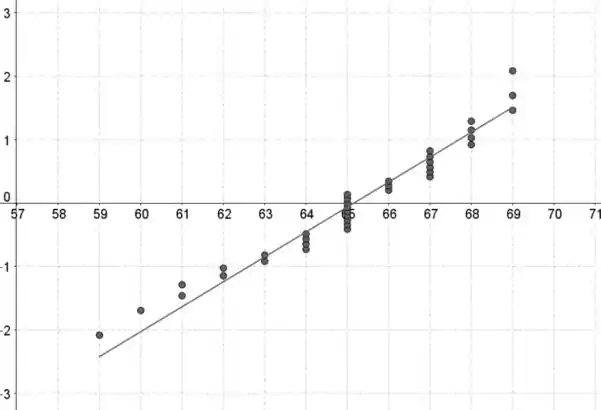
Passo 3
Para os homens:
Os valores dos dados estão no eixo horizontal e o padrão dos valores normais estão no eixo vertical.
Se os dados contiverem n valores de dados, então os valores normais padronizadas são os valores na tabela III correspondente a uma área de (ou a área mais próxima) com
O menor valor padronizado corresponde ao menor valor de dados, o segundo menor valor padronizado corresponde ao segundo menor valor de dados e assim por diante.
Passo 4
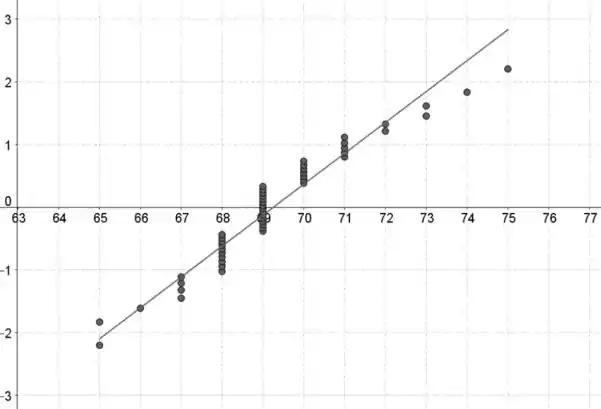
Parece razoável supor que ambas as distribuições de dados são normalmente distribuídas, porque o padrão nos gráficos de probabilidade normais são aproximadamente lineares.
Se combinarmos os dois gráficos de probabilidade normal, então notamos que as distribuições parecem ter a mesma inclinação.
Passo 5
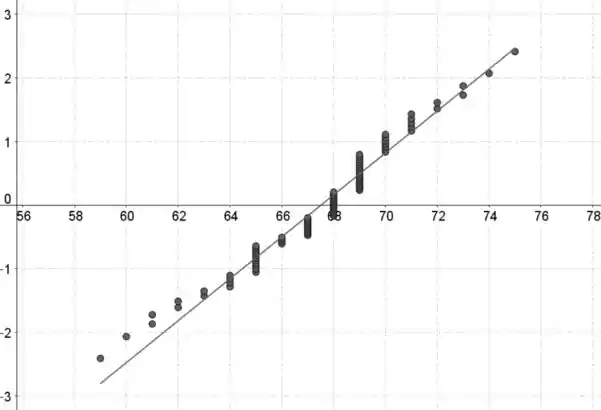
Parece razoável supor que ambas as distribuições de dados são normalmente distribuídas.
Resposta
Parece razoável supor que ambas as distribuições de dados são normalmente distribuídas.