Enunciado
Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 16.Problemas - Ex. 22a
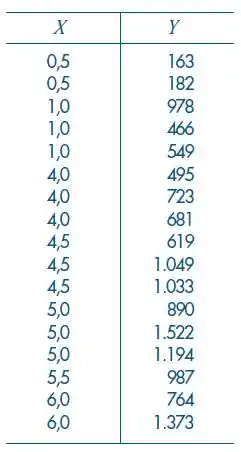
O custo de manutenção de tratores parece aumentar com a idade do trator. Os seguintes dados foram obtidos (representa idade em anos e o custo por seis meses):
- Ajuste o modelo e teste a hipótese de interesse para o nível.
Passo 1
Vamos ajustar a reta , em que representa o coeficiente da regressão que representa o intercepto da reta e representa o coeficiente da regressão que representa a inclinação da reta.
De acordo com a equação , podemos encontrar os coeficientes da equação da reta, através dos cálculos:
Portanto, .
Agora, vamos testar a hipótese de interesse para o nível
Neste caso,
Sob , rejeitamos a hipótese
Resposta
Assim, conclui-se o desejado.
Exercícios de Livros Relacionados
11-22.Considere os dados do Exercicio 11-2 sobre x- lemperatura dasuperticie da estrada e y - deflexão no pavimento.a) Teste a significância da regressão. usande a=0.05. Encontre o valorP para esse te
11-17. Considere o modelo de regrexsáo desenvolvido no Exercicio 11.6. Suponha que o deslocamento do motor fosse medido em centimetroscúbicos em vez de polegadas cúbicas.a) Escreva o novo modeio de re
11-21. Considere os dados do Exercício 11-1 sobre .x - tensáo a com-pressáo e y - permeabilidade intrinseea de concreto.a) Teste a significancia da regressao, usando x-0.05. Encontre o valorP para ess
11-20. Suponha que desejemos ajustar um modelo de regressão para oqual a verdadcira linha de regressão passa através do ponto (0.0).0modelo apropriado é. Considere ue temos n pares de dadosa) Encontie
11-19. Considere o moxlelo de regressáo linear simples:Y = β 0 + β 1 x + ϵ Suponha que o analista qucira usar : - x - X como o regressor.a) Usando os dados no Exercício I1-11, consrua un gráfico de di