Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 11.Exercícios - Ex. 19

11-19. Considere o moxlelo de regressáo linear simples:   Y = β 0 + β 1 x + ϵ

Suponha que o analista qucira usar : - x - X como o regressor.

a) Usando os dados no Exercício I1-11, consrua un gráfico de disper-

são dos pontos (x.v) e então um outro dos pontos

Use os dois gráficos para explicar intuitivamente como os dois mo-

Delos Y - β 0 + β 1 x + c  e  Y - β 0 * + β i * + ϵ estão relacionados.

b) Encontre as estimativas de minimos quadrados de no mode-

lo. Y = β i * + β i * z + ϵ Comoelas estão relacionadas às estimativas de

mínimos quadrados?

Passo 1

Oi oi gente,

Vamos lá fazer mais uma questão passo a passo?

Vem comigo!

Letra a:

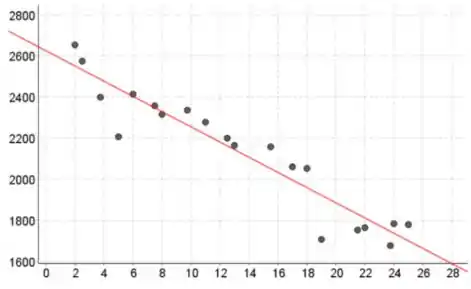
x está no eixo horizontal e y está no eixo vertical.

x - x _ está no eixo horizontal e y está no eixo vertical.

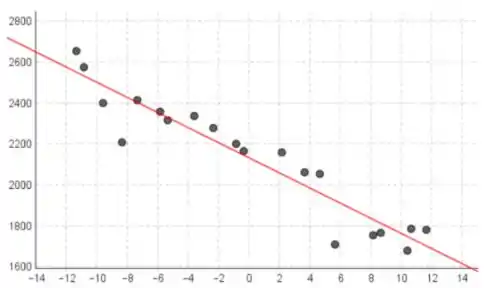
Notamos que os dois gráficos de dispersão são iguais, com exceção da escala no eixo horizontal. Isso indica que a linha de regressão Y = β 0 * + β 1 * z + ϵ é a linha de regressão Y = β 0 + β 1 x + ϵ traduzido à esquerda por unidades x _

Passo 2

Letra b:

A linha de regressão   Y = β 0 + β 1 * z + ϵ é a linha de regressão Y = β 0 + β 1 x + ϵ e traduzida para baixo em x _ unidades. Isso significa que a inclinação das linhas de regressão são as mesmas. O que também é verdadeiro para suas estimativas :

β ^ 1 * = β ^ 1

A linha de regressão   Y = β 0 * + β 1 * z + ϵ é a linha de regressão Y = β 0 + β 1 x + ϵ e traduzida para baixo em x _ unidades. Isso significa que a constante Y = β 0 * + β 1 * z + ϵ da linha de regressão Y = β 0 + β 1 x + ϵ é diminuída pela média da amostra x _ , o que também é verdadeiro para suas estimativas:

β ^ 0 * = β ^ 0 - x -

Resposta

  1. Notamos que os dois gráficos de dispersão são iguais, com exceção da escala no eixo horizontal. Isso indica que a linha de regressão Y = β 0 * + β 1 * z + ϵ é a linha de regressão Y = β 0 + β 1 x + ϵ traduzido à esquerda por unidades x _
  2. β ^ 1 * = β ^ 1  e  β ^ 0 * = β ^ 0 - x -
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

11.18. Mostre que em um moxlelo de regressäo linear simples. o ponto (F. y) exatamente sobre a linha de regressão dos mínimos quadrados.
11-22.Considere os dados do Exercicio 11-2 sobre x- lemperatura dasuperticie da estrada e y - deflexão no pavimento.a) Teste a significância da regressão. usande a=0.05. Encontre o valorP para esse te
11-17. Considere o modelo de regrexsáo desenvolvido no Exercicio 11.6. Suponha que o deslocamento do motor fosse medido em centimetroscúbicos em vez de polegadas cúbicas.a) Escreva o novo modeio de re
11-21. Considere os dados do Exercício 11-1 sobre .x - tensáo a com-pressáo e y - permeabilidade intrinseea de concreto.a) Teste a significancia da regressao, usando x-0.05. Encontre o valorP para ess
11-20. Suponha que desejemos ajustar um modelo de regressão para oqual a verdadcira linha de regressão passa através do ponto (0.0).0modelo apropriado é. Considere ue temos n pares de dadosa) Encontie