Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 9.6 - Ex. 19b

O custo de manutenção de treminhões movidos a gasolina e a diesel são dados abaixo para duas amostras aleatórias de 10 treminhões de cada tipo. Os veículos considerados trafegam sob as mesmas condições em uma mesma área.

  1. Verifique se as variâncias dos dois grupos são semelhantes.

Passo 1

Continuando nessa saga que chamamos de exercício...

Nesse item B, vamos ter que realizar um teste para a diferença entre as variâncias.

Sempre muito bom lembrar que estamos estudando a seguinte variável:

X = C u s t o   d e   m a n u t e n ç ã o   p a r a   T r e m i n h õ e s .  

Com isso, para realizar o teste entre as amostra, precisaremos utilizar a seguinte aproximação:

F = S D 2 / σ D 2 S G 2 / σ G 2 ~ F n D - 1 ; n G - 1

Trata-se de uma distribuição F   d e   S n e d e c o r com n D - 1 ; n G - 1 graus de liberdade.

Vale ressaltar a importância de manter essa ordem nos graus, pois o primeiro refere-se a quem está no numerador (diesel) e o segundo a quem está no denominador (gasolina).

Se por acaso você inverter os dados, colocar gasolina no numerador e diesel no denominador vai precisar também inverter os graus; Capithe?

Passo 2

Ta legal, vamos agora encontrar quem é a nossa variância amostral S 2 ; mas para achar ela precisamos também da média amostral, vamos a isso então:

X - D = ∑ i = 1 10 x i n = 79,16 10 = 7 , 8 2

E a variância do Diesel:

S D 2 = ∑ i = 1 10 x i 2 - n D X - D 2 n D - 1 = 795,79 - 10 7 , 8 2 2 9 ≅ 20,47

Agora para a gasolina:

X - G = 88,04 10 ≅ 8,80

E a variância:

S G 2 = 952,55 - ( 10 ) ( 8,80 2 ) 9 ≅ 19,79

Podia acabar aqui já, mó trampo cara!

Passo 3

Mas ainda precisamos testar se:

H 0 : σ D 2 - σ G 2 = 0         c o n t r a           H 1 :   σ D 2 - σ G 2 ≠ 0

Para isso vamos precisar da nossa região crítica, adotando α = 5 % :

R C = f 0 ∈ R f 0 < - f 1 - α 2 ; n D - 1 ; n G - 1       o u     f 0 >   f α 2 ; n D - 1 ; n G - 1    

Veja bem, queremos um valor f α 2 ; n D - 1 ; n G - 1 tal que:

P F > f α 2 ; n D - 1 ; n G - 1 = α 2 = 0,025

Isso significa que precisaremos ir na tabela F   a 2,5 % , e buscar a intersecção da coluna 10 - 1 = 9   graus de liberdade, com a linha 10 - 1 = 9 graus de liberdade:

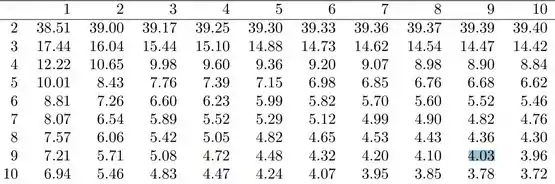
Ou seja, encontramos:

f 0,025 ; 9 ; 9 = 4,03

Agora, falta encontrar o f 1 - α 2 ; n D - 1 ; n G - 1 , para acha-lo basta fazer o seguinte:

f 1 - α 2 ; n D - 1 ; n G - 1 = 1 f α 2 ; n G - 1 ; n D - 1

E trazendo pro nosso exercício:

f 0,975 ; 9 ; 9 = 1 f 0,025 ; 9 ; 9 = 1 4,03 ≅ 0,248

Uma coisa muito importante agora!! Pay attention: ali no denominador nós vamos inverter os graus de liberdade propositadamente...

Lembre-se sempre disso, a tabela F   só nos da a chance de termos um número na cauda superior,

Isso significa que para obter a extremidade inferior em uma distribuição F   d e   s n e d e c o r precisamos tomar o inverso da extremidade superior invertendo os graus de liberdade.

Calma, aos poucos você pega o jeito.

Portanto a nossa região crítica fica assim:

R C = f 0 < - 0,248       o u       f 0 > 4,03

Finalmente, só falta realizar o teste sob a hipótese nula:

F = S D 2 / σ D 2 S G 2 / σ G 2

Como na hipótese nula, σ D 2 = σ G 2 , então teremos:

f 0 = S D 2 S G 2 = 20,47 19,79 ≅ 1,034

Podemos então concluir que, como f 0 = 1,034 NÃO pertence a região crítica, devemos ACEITAR a hipótese nula.

Resposta

Concluindo, existem evidencias de que as variâncias populacionais das duas amostras sejam iguais.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Estimação numa distribuição uniforme. Suponha que X tenha uma distribuição uniforme no intervalo (0, θ), onde θ é desconhecido. Uma amostra de n observações X1, ..., Xn é escolhida. Sabemos que E(X) =
Estão sendo estudados dois processos para conservar alimentos, cuja principal variável de interesse é o tempo de duração destes. No processo A, o tempo X de duração segue a distribuição N(μA, 100), e
Continuação do Problema 37.Outra maneira de estimar θ na uniforme é a seguinte. Considere M = max(X1, ..., Xn) = x(n), ou seja, o maior valor da amostra. Para qualquer valor de θ, M T2 é consistente?
Para os Problemas 37 e 38, mostre que Var(T2) = [3/(n + 2)] Var(T1). Tome n = 1, 2, 10, 50, 100 e verifique qual a relação entre as duas variâncias. Verifique que, para n grande, T2= [(n + 1)/n]M é um
Estimação numa distribuição uniforme. Suponha que X tenha uma distribuição uniforme no intervalo (0, θ), onde θ é desconhecido. Uma amostra de n observações X1, ..., Xn é escolhida. Sabemos que E(X) =