Enunciado
Probabilidade e Estatística - Walpole - Probabilidade e Estatística para Engenharia e Ciências- Ed: 8º - Capítulo 1.Exercícios - Ex. 24
Os dados históricos seguintes são os salários de pessoal (dólares por aluno) em 30 escolas amostradas no lado oeste dos Estados Unidos, no início dos anos 70.
3,79 2,99 2,77 2,91 3,10 1,84 2,52 3,22 2,45 2,14 2,67 2,52 2,71 2,75 3,57 3,85 3,36 2,05 2,89 2,83 3,13 2,44 2,10 3,71 3,14 3,54 2,37 2,68 3,51 3,37
(a) Calcule a média e o desvio-padrão amostrais.
(b) Construa um histograma de frequências relativas dos dados.
(c) Construa um diagrama de ramo-e-folhas dos dados.
Passo 1
Os dados que são informados no enunciado são os salários dos funcionários, dólares por aluno.
Com escolas no início dos anos 1970.
Passo 2
Para definirmos a média amostral temos a seguinte equação:
Então, temos o somatório de todos os dados da tabela dividido pelo número de escolas.
A variância da amostra dada por:
Substituindo os valores:
Por fim, o desvio padrão da amostra é a raiz quadrada da variância:
Passo 3
Para montarmos o histograma de frequências relativas, temos que analisar com qual frequência os dados em cada intervalo aparecem, neste caso, podemos notar que entre o período e só aparece o sendo menos de das vezes. O histograma pode ser analisado abaixo:
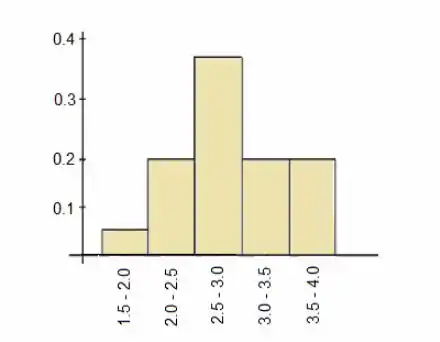
Passo 4
Vamos deixar o primeiro dígito à esquerda e o primeiro dígito à direita do ponto decimal formarem um ramo. Assim, os ramos serão 18, 20, 21, 23, 24,... 37 e 38. (por exemplo, um valor 3,79 terá um valor de ramo de 37 e folha 9.)
O diagrama de ramo-e-folhas dos dados está definido abaixo:
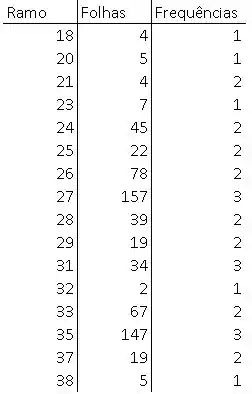
Resposta
(a) ; .
(b) Passo 3.
(c) Passo 4.