Determine o valor de se a área abaixo da curva normal padrão

(a) à direita de é 0,3622;

(b) à esquerda de é 0,1131;

(c) entre 0 e , com , é 0,4838;

(d) entre - 2 e , com , é 0,9500.

Show, agora que relembramos a teoria, faremos o item a)

Neste item ele nos diz: sabendo que a área é igual a 0,3622, quanto vale

Ele achou que complicaria as coisas para a gente, MAS, nós sabemos muito bem como prosseguir.

Se nós temos um , andando pela tabela nós conseguimos descobrir a área a sua esquerda.

Então nesse item, nós faremos o processo inverso, nós temos uma área que está na tabela e encontraremos seu, a partir dela.

Entretanto, no enunciado ele nos pede a área a direita deste determinado

Logo, usemos:

Manipulando:

Com esse resultado nos concluímos que a área a esquerda de nosso vale .

Agora, basta procurar nosso na tabela.

E encontraremos

Agora vamos ao item b)

Neste item ele nos pede dizendo que a área a sua esquerda vale 0,1131.

Ou seja, o problema aqui é ainda mais fácil, ele já nos deu a área a esquerda de só precisamos procurar na tabela.

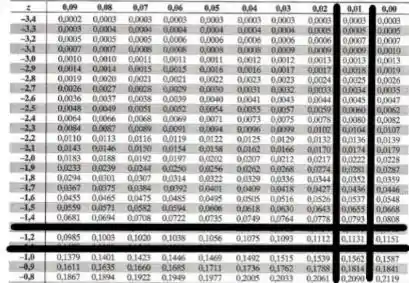
E desse modo, encontramos

Agora vamos ao item c)

Queremos determinar, sabendo que a área entre 0 e , com , é 0,4838

Vamos aplicar alguns macetes para resolver:

E agora manipulando:

Nesse último passo eu simplesmente isolei a variável que queria descobrir, e substitui o valor tabelado para .

Agora, nós temos o valor da área a esquerda de um determinado , para descobrir quanto vale , precisamos fazer igual no item b), simplesmente procurar na tabela.

Desse modo encontraremos

Por último, vamos ao item d)

Queremos determinar , sabendo que a área entre - 2 e , com , é 0,9500

Logo, vamos aplicar a mesma estratégia do item c)

Manipulando:

Nesse último passo eu simplesmente isolei a variável que queria descobrir, e substitui o valor tabelado para

Agora, nós temos o valor da área a esquerda de um determinado , para descobrir quanto vale , precisamos simplesmente procurar na tabela.

Desse modo encontraremos