Enunciado
Probabilidade e Estatística - Walpole - Probabilidade e Estatística para Engenharia e Ciências- Ed: 8º - Capítulo 10.Exercícios - Ex. 93
Um criminologista conduziu uma pesquisa para determinar se a incidência de certos tipos de crime varia de acordo com a região de uma cidade grande. Os tipos de crime de interesse são: agressão, arrombamento, roubo e homicídio. A tabela a seguir mostra o número de crimes cometidos em quatro áreas da cidade no ano passado.
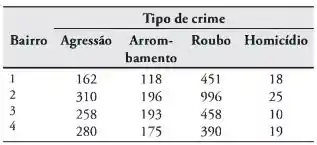
Podemos concluir, com base nesses dados, num nível de significância de 0,01, que a ocorrência desses tipos de crime depende da área da cidade?
Passo 1
Falaiii meus amores, cêis tão suave?
“Se alguma coisa está dificil de ser feita, é porque não é para ser feita" # sóquenão”
Testar
O nível de significância especificado é
Vamos considerar a seguinte tabela
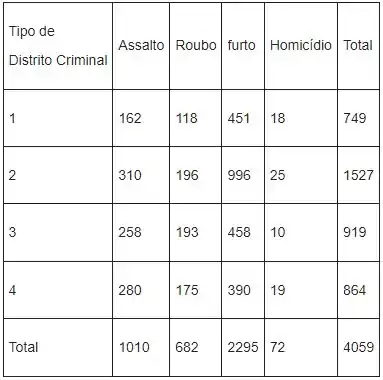
A regra geral para obtenção da frequência esperada de qualquer célula é dada pela seguinte maneira:
Na tabela a seguir, mostraremos a frequência observada junto com a frequência esperada ente colchetes para cada célula
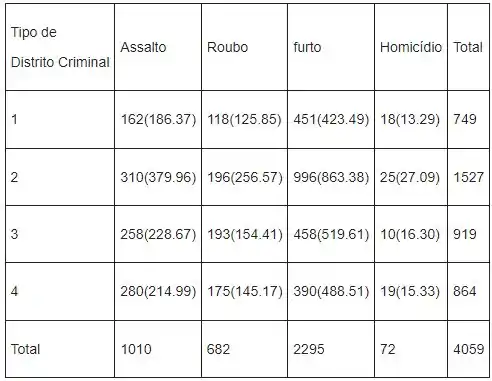
A estatística do teste qui-quadrado é dada como
Sob a estatística de teste segue a distribuição de com graus de liberdade, pois há duas linhas e duas colunas.
Passo 2
A região crítica é dada como onde é o ponto 0.01 superior da distribuição com 9 graus de liberdade.
O valor tabelado de é 21.666
Portanto, rejeitamos e concluímos que a ocorrência destes tipos de crimes é dependente do bairro da cidade.
Certo, cérebro, eu não gosto de você e nem você de mim, então faça tudo certo pelo menos uma vez para que eu possa continuar te matando com estudos, certo?
Resposta
Portanto, rejeitamos e concluímos que a ocorrência destes tipos de crimes é dependente do bairro da cidade.