Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Walpole - Probabilidade e Estatística para Engenharia e Ciências- Ed: 8º - Capítulo 10.Exercícios - Ex. 84

Três pedras são selecionadas de uma urna com cinco pedras vermelhas e três verdes. Depois de registrado o número X de pedras vermelhas, as pedras são repostas na urna e o experimento é repetido 112 vezes. Os resultados estão a seguir:

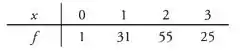
Teste a hipótese no nível de significância de 0,05 de que os dados registrados podem ser ajustados pela distribuição hipergeométrica h ( x ; 8 ,   3 ,   5 ) ,   x =   0 ,   1 ,   2 ,   3 .

Passo 1

E aí meus queridos? Tudo certinho?

“Operador! Me dê o número do responde ai!.... Preciso resolver essa questão”

Pelas informações, observe que a urna contém 5 bolinhas vermelhas e 3 bolinhas verdes.

Três bolas de gude são selecionadas da urna.

Considere que X é a variável aleatória que representa o número de bolas sorteadas é vermelho.

O experimento repetido 112 vezes.

Portanto, a distribuição de frequência é a seguinte:

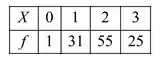
A variável aleatória X segue distribuição hipergeométrica com parâmetros N   =   8 , n = 3 , k = 5

A função de massa de probabilidade da distribuição hipergeométrica é a seguinte:

H x : N , n , k = k 0 N - k n - 0 N n

= 5 1 8 - 5 3 - 0 8 3

= 1 56

P X = 1 = k 1 N - k n - 1 N n

= 5 1 8 - 5 3 - 1 8 3

= 5 × 3 56

= 15 56

Passo 2

P X = 2 = k 2 N - k n - 2 N n

= 5 2 8 - 5 3 - 2 8 3

= 10 × 3 56

= 30 56

P X = 3 = k 3 N - k n - 3 N n

= 5 3 8 - 5 3 - 3 8 3

= 10 × 1 56

= 1 0 56

Passo 3

Calcularemos as frequências esperadas para cada valor x

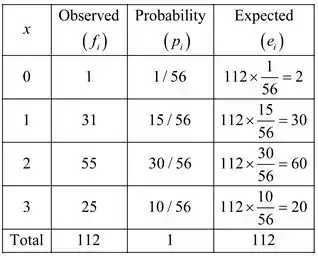
Verifique se os dados registrados se ajustam aos dados hipergeométricos ou não.

A hipótese nula e alternativa é a seguinte:

Hipótese nula,

H 0 :   o s   d a d o s   r e g i s t r a d o s   s ã o   a j u s t a d o s   p a r a   a   d i s t r i b u i ç ã o   h i p e r g e o m é t r i c a .

Hipótese alternativa,

H 1 :   o s   d a d o s   r e g i s t r a d o s   n ã o   s ã o   a j u s t a d o s   p a r a   a   d i s t r i b u i ç ã o   h i p e r g e o m é t r i c a .

O nível de significância é, α   =   0.05

Calcular estatística de teste.

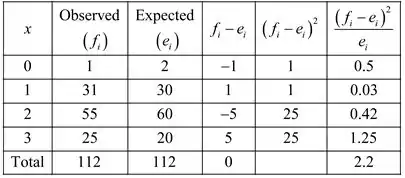
Pela tabela, observe que o valor calculado da estatística de teste é

x c a l 2 = ∑ f i - e i 2 e i = 2.20

Passo 4

Os graus de liberdade são,

d f   =   4 - 1

= 4 - 1

=   3

O nível de significância é, α   =   0.05

A partir dos valores padrão da tabela Qui-quadrado, observe que o valor crítico de x 2 no nível de significância de 5% e 3 graus de liberdade é, x 0,05 2 =   7.81

Compare o valor calculado da estatística do teste qui-quadrado com seu respectivo valor crítico.

Aqui, o valor calculado menor que o valor crítico falho em rejeitar a hipótese nula.

Portanto, conclua que os dados registrados são ajustados para a distribuição hipergeométrica.

"Se algo é difícil de fazer, vale a pena ser feito!"

Resposta

Portanto, conclua que os dados registrados são ajustados para a distribuição hipergeométrica.

Exercícios de Livros Relacionados

A cada um, de um grupo de 20 jogadores de tênis intermediários, são dadas duas raquetes, uma com cordas de náilon e outra com cordas de tripa sintética. Após várias semanas jogando com as duas raquete
A biblioteca de uma universidade rotineiramente faz o inventário completo das prateleiras uma vez por ano. Devido às novas regras de armazenamento nas prateleiras instituídas no ano anterior, o biblio
Os registros de DMV do estado indicam que, de todos os veículos que se submeteram ao teste de emissões durante o ano anterior, 70 % passaram na primeira tentativa. Uma amostra aleatória de 200 carros
Um fabricante de baterias de níquel hidrogênio seleciona aleatoriamente 100 placas de níquel para testar as células, ciclando-as certa quantidade de vezes e determinando que 14 placas foram cobertas d
Em 60 lances de uma moeda observaram-se 37 caras. Testar a hipótese da moeda ser honesta, aos níveis de 5% e 1%.