Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 13.Exercícios - Ex. 6

Os dados a seguir sobre x = densidade real k g / m m 3 e y = quantidade de umidade (क d.b.) foram reproduzidos de um gráfico do artigo "Physical Properties of Cumin Seed" (J. Agric. Engr. Res., 1996, p. 93-98).A equação da reta dos mínimos quadrados é y = 1.008,14 + 6,19268 x (essa equação difere muito ligeiramente da equaçāo apresentada no artigo); s = 7,265 e r 2 = 0,968 .

a. Realize um teste de utilidade do modelo e comente.

b. Calcule os valores dos resíduos e represente-os graficamente em relação a x . O gráfico sugere que uma função de regressão linear é imprópria?

c. Calcule os valores dos resíduos padronizados e represente-0s graficamente em relação a x . Existe algum resíduo padronizado extraordinariamente grande (positivo ou negativo)? Esse gráfico fornece a mesma mensagem que o gráfico da parte (b) em relação à aplicabilidade da função de regressão linear?

Passo 1

Realize um teste de utilidade do modelo e comente

a. H a : β 1 = 0   v s .   H a : β 1 ≠ 0 , o teste estatístico é t = β ^ 1 s β ^ e rejeitaremos H 0 se t ≥ t 025,4 = 2.776   o u   s e     t ≤ - 2.776 ⋅ s A ^ 1 = s S x x = 7.265 12.869 = . 565 e t = 6.19268 . 565 = 10.97 .   U m a   v e z   q u e   10.97 ≥ 2.776 , rejeitaremos H 0 e concluímos que o modelo é utilizável

Passo 2

Calcule os valores dos resíduos e represente-os graficamente em relação a x . O gráfico sugere que uma função de regressão linear é imprópria?

b. y ^ ( 7.0 ) = 1008.14 + 6.19268 ( 7.0 ) = 1051.49 , do qual o resíduo é y - y ^ ( 7.0 ) = 1046 - 1051.49 = - 5.49 . Da mesma forma, os outros resíduos são 73,4.11 , 7.91,3.58 ,   e - 9.38

O gráfico dos resíduos vs x segue:

Como um padrão curvo aparece, uma função de regressão linear pode ser inadequada.

Passo 3

c. Os resíduos padronizados são calculados como

e 1 * = - 5.49 7.265 1 + 1 6 + ( 7.0 - 14.48 ) 2 165.5983 = - 1.074 e, similarmente, os outros são - . 123   . 624,1.208 , . 587 ,   a n d   - 1.841

O gráfico de e * v 5 x segue :

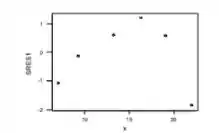
Este gráfico fornece a mesma informação que o gráfico anterior. Nenhum valor é excepcionalmente grande, mas o e * de -1,841 está próximo a 2 desvios padrão do valor esperado de 0

Resposta

a. 10.97 ≥ 2.776 , rejeitaremos H 0 e concluímos que o modelo é utilizável

b. Como um padrão curvo aparece, uma função de regressão linear pode ser inadequada.

c. Este gráfico fornece a mesma informação que o gráfico anterior. Nenhum valor é excepcionalmente grande, mas o e * de -1,841 está próximo a 2 desvios padrão do valor esperado de 0

Exercícios de Livros Relacionados

Uma amostra de n = 20 empresas foi selecionada e foram determinados os valores de y = preço da açāo e k = 15 variáveis de previsāo (como dividendo trimestral, lucros do ano anterior, quociente da dívi
Visto que R 2 = 0,723 para o modelo contendo os previsores x 1 , x 4 , x 5 e x 8 e R 2 = 0,689 no modelo com os previsores x 1 , x 3 , x 5 e x 6 o que você pode dizer sobre R 2 no modelo contendo os p
A exposição à poluição atmosférica diminui a expectativa de vida? Essa pergunta foi examinada no artigo "Does Air Pollution Shorten Lives?" (Statistics and Public Policy, Reading, MA, Addison Wesley,
a. Uma regressão linear poderia resultar nos resíduos 23, 27, 5, 17, 8, 9 e 15? Por quê? b. Uma regressão linear poderia resultar nos resíduos 23, 27, 5, 17, 8, 12 e 2 correspondentes aos valores x 3,
Lembre-se de que ˆ 0 ˆ 1x tem uma distribuição normal, com valor esperado 0 1x e variância de modo que tem uma distribuição normal padronizada. Se S SQE/(n2) for substituída por , a variável resultant