Enunciado
Probabilidade e Estatística - Estatistica Mauri Guerra estatistica indutiva- Ed: 1º - Capítulo 13.Exercícios propostos - Ex. 3c
Os dados da tabela referem-se a um grupo de 11 casas alugadas:
Pede-se:
- Calcular os coeficientes de explicação e correlação e testar a existência dessas regressões, ao nível de significância de .
Passo 1
Olá galerinha, tudo bem com vocês? Primeiramente vamos relembrar os dados obtidos nos itens a e b:
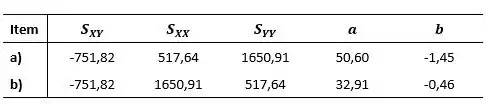
Ajustar uma reta a valores observados de 2 variáveis é sempre possível, porém não podemos garantir que existe regressão entre as mesmas, nem se o modelo teórico ajustado tem um bom poder de explicação da realidade. Então precisamos testados através do estudo da Análise de Variância e do Coeficiente de Explicação. Temos o seguinte:
Se , existe a regressão de sobre .
O coeficiente de explicação é calculado por:
E o coeficiente de correlação:
Para todos os itens, teremos os mesmos graus de liberdade:
- ;
- ;
- .
Então, para , nosso tabelado será:
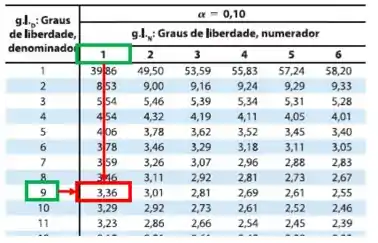
Passo 2
Então vamos lá para nosso exercício. Para o item a) temos:
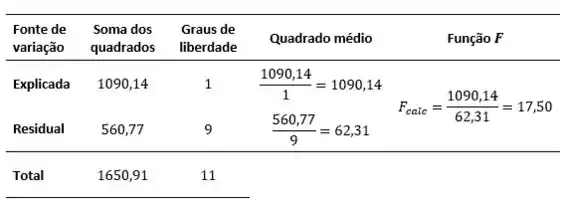
Como (), então existe regressão.
Agora irmos calcular os coeficientes de explicação e correlação, respectivamente:
Passo 3
E para o item b):
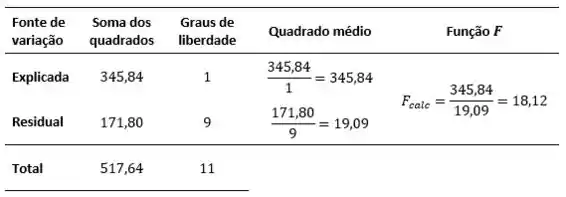
Como (), então existe regressão.
Agora irmos calcular os coeficientes de explicação e correlação, respectivamente:
Esse já acabou pessoal, te espero em mais exercícios. Até mais!
Resposta
As 2 regressões existem, num nível de significância de 10%;
- ;
- .