Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Estatistica Mauri Guerra estatistica indutiva- Ed: 1º - Capítulo 13.Exercícios propostos - Ex. 2a

A tabela abaixo apresenta o número de acidentes de estrada ocorridos e o número de veículos licenciados, num certo país, no período 1957/1967:

Pede-se:

  1. Ajustar uma reta de mínimos quadrados do número de acidentes em função do tempo;

Passo 1

Olá galerinha, tudo bem com vocês? Primeiramente iremos relembrar a teoria.

O método dos mínimos quadrados é um dos métodos utilizados para estimar os parâmetros da regressão. Onde iremos estimar os parâmetros α e β da reta da regressão, e chamaremos de a e b , respectivamente. Sendo assim:

  • Y = α + β ∙ X reta de regressão de Y sobre X ;
  • Y ^ = a + b ∙ X estimativa da reta de regressão.

O método dos mínimos quadrados fornece os valores de a e b tais que ∑ Y i - Y ^ i 2 seja mínimo. Iremos descobrir os valores de a e b pela Regra de Cramer. Para isso, iremos utilizar algumas equações:

  • Os valores médios de X i e Y i :

    • X - = ∑ X i n

    Y - = ∑ Y i n

  • As variâncias são calculadas pelas seguintes equações:

    • S X Y = ∑ ( X i ∙ Y i ) - ∑ X i ∙ ∑ Y i n

    S X X = ∑ X i 2 - ∑ X i 2 n

    S Y Y = ∑ Y i 2 - ∑ Y i 2 n

  • E as estimativas procuradas de a e b :

b = S X Y S X X

a = Y - - b ∙ X -

Passo 2

Sendo assim, iremos iniciar nosso exercício, primeiramente precisamos relembrar que qualquer série de valores de uma variável colocada em função do tempo constitui o que se chama de série temporal. Para essas séries é sempre conveniente estabelecer uma escala qualquer de tempo ( X ) com número em progressão aritmética, de preferência números que a soma seja igual a zero, pois os cálculos serão simplificados, então:

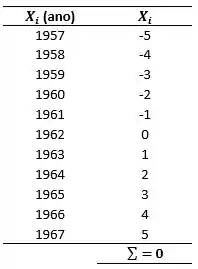
Agora conseguimos calcular os valores de S X Y , S X X e S Y Y :

S X Y = 1358 - 0 ∙ 2396 11 = 1358

S X X = 110 - 0 2 11 = 110

S Y Y = 539512 - 2396 2 11 = 17619,64

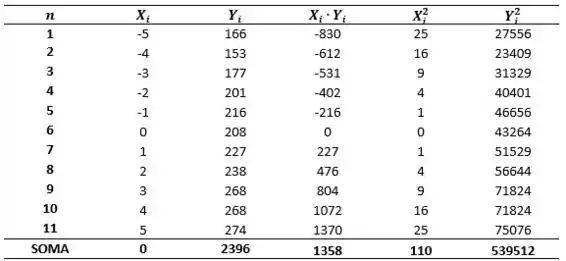
Passo 3

Neste próximo passo iremos calcular as médias de X i e Y i :

X - = 0 11 = 0

Y - = 2396 11 = 217,82

Passo 4

E por fim, iremos obter os valores de a e b , para obtermos a equação da reta:

b = 1358 110 = 12,35

a = 217,82 - 12,35 ∙ 0 = 217,82

Sendo assim:

Y ^ = 217,82 + 12,35 ∙ X

Prontinho pessoal, até mais!

Resposta

Y ^ = 217,82 + 12,35 ∙ X .

Exercícios de Livros Relacionados

Sejam s x e s y os desvios padrão amostrais dos xs e ys observados, respectivamente [portanto, s x 2 = ∑ x i - x ¯ 2 n - 1 e algo semelhante pode-se afirmar em relação a s2 y ].
Na Seção 12.4, apresentamos uma fórmula para V( ˆ 0 ˆ 1x*) e um IC para 0 1x*. Tomando x* 0, obtemos 2 ˆ 0 e um IC para 0. Use os dados do Exemplo 12.11 para calcular o desvio padrão estimado de ˆ 0 e
Processos normais de criação de peixes em aquaculturas inevitavelmente deixam os peixes estressados, o que pode influenciar negativamente no crescimento, na reprodução, na qualidade da carne e na susc
Na biofiltragem de esgoto, o ar descarregado de uma ins-talação de tratamento passa através de uma membrana porosa úmida que faz com que os contaminantes dissolvam-se na água e sejam transformados em
Reconsidere a situação do Exercício 68, no qual x = % de entrada térmica de RDF e y = % de eficiência de uma determinada caldeira foram relacionadas por meio de um modelo de regressão linear simples.