Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Estatistica Mauri Guerra estatistica indutiva- Ed: 1º - Capítulo 13.Exercícios propostos - Ex. 3d

Os dados da tabela referem-se a um grupo de 11 casas alugadas:

Pede-se:

  1. Construir os intervalos de confiança para f ( X i ) e Y i , com relação a regressão do item (a), para X i = 30 , com α = 10 % .

Passo 1

Olá galerinha, tudo bem com vocês? Vem comigo que eu vou te ajudar!

Como a variância populacional σ 2 é desconhecida, iremos substituí-la pelo seu estimador amostral S 2 :

S 2 = S Y Y - b ∙ S X Y n - 2

O intervalo de confiança para f ( x ) :

Y ^ i - t ∙ S ∙ 1 n + ( X i - X - ) 2 S X X   ≤ f X i ≤   Y ^ i + t ∙ S ∙ 1 n + ( X i - X - ) 2 S X X  

E para Y :

Y ^ i - t ∙ S ∙ 1 + 1 n + ( X i - X - ) 2 S X X   ≤ Y i ≤ Y ^ i + t ∙ S ∙ 1 + 1 n + ( X i - X - ) 2 S X X

Para o cálculo dos intervalos de confiança α e β , iremos substituir a variável normal pela variável “t” de Student, a qual tem G L = n - 2 = 9 graus de liberdade. Então, pela tabela da distribuição t, com α = 0 , 10 , temos:

t = 1,833

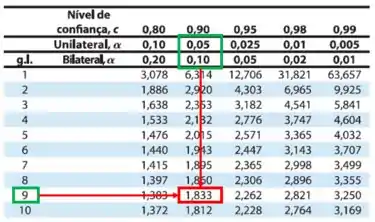
Passo 2

Do item a) temos os seguintes resultados:

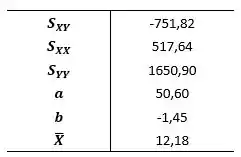
Onde:

Y ^ = 50,60 - 1,45 ∙ X

Então:

S = 1 650,91 - ( - 1,45 ) ∙ ( - 751,82 ) 11 - 2 = 7,89

Passo 3

Para X i = 30 , temos:

Y ^ = 50,60 - 1,45 ∙ 30 = 7,1

Com todos os dados conseguimos calcular o intervalo de confiança para f ( x ) :

  f X i =   7,1 ± 1,833 ∙ 7,89 ∙ 1 11 + ( 30 - 12,18 ) 2 517,64  

- 5 , 0 4 ≤   f X i ≤ 19,24

E para Y :

Y i =   7,1 ± 1,833 ∙ 7,89 ∙ 1 + 1 11 + ( 30 - 12,18 ) 2 517,64  

- 11,78   ≤ Y i ≤ 25,98

Prontinho pessoal, até mais!

Resposta

- 5,04 ≤   f X i ≤ 19,24 ;

- 11,78   ≤ Y i ≤ 25,98 .

Exercícios de Livros Relacionados

Os dados a seguir foram reproduzidos de um gráfico de dispersão apresentado no artigo “Urban Emissions Measured with Aircraft” (J. of the Air and Waste Mgmt. Assoc., 1998, p. 16–25). A variável de res
Os dados a seguir sobre x = taxa de consumo de óleo diesel pelo método de peso líquido e y = taxa medida pelo método de traçado de IC, ambos em g/h, foram reproduzidos de um gráfico apresentado no art
Os dados a seguir são um subconjunto dos dados apresentados no artigo “Radial Tension Strength of Pipe and Other Curved Flexural Members” (J. Amer. Concrete Inst., 1980, p. 33–39). As variáveis são te
A presença de carbetos de liga dura em ligas de ferro de cromo branco alto produz uma excelente resistência à abrasão, o que as torna adequadas à manipulação de materiais na mineração e às indústrias
O resultado do SAS apresentado a seguir baseia-se em dados extraídos do artigo “Evidence for and the Rate of Denitrification in the Arabian Sea” (Deep Sea Research, 1978, p. 431–435). As variáveis em