Enunciado

Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 9.6 - Ex. 3

O desempenho em duas classes de Estatística está sendo comparado através do resultado dos dez melhores alunos de cada turma.

Admitindo que as variabilidades das classes são iguais, pode ser dito que elas têm o mesmo desempenho médio? Faça as suposições necessárias e utilize

Passo 1

Fala ai meu querido, vamos resolver essa questão rapidinho, ok? Trata-se de uma questão que se encaixa no 3A da seção 9.2 desse capítulo, e vou usar uma planilha de Excel com a ferramenta “Análise de Dados” ativada.

Passo 2

A ferramenta análise de dados possui uma função chamda “Teste-t: duas amostras presumindo variâncias equivalentes” que nos provêm os seguintes valores para essas amostragens:

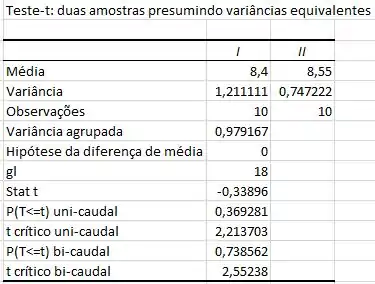
Passo 3

Como nosso teste de hipótese é:

Temos um teste bi-caudal e precisamos calcular nosso :

Sendo:

Calculando esses valores, você irá encontrar:

Que é o valor que o Excel chama de Stat t.

Passo 4

Com , temos que nossa região crítica é , portanto nosso está dentro da área de aceitação, e podemos afirmar que não existe diferença entre o desempenho médio dos alunos.