O salário de recém formados em Veterinária foi amostrado em duas cidades. Na cidade A, 10 profissionais foram sorteados e na cidade B, 15. Os resultados em salários mínimos, são apresentados a seguir:

Admitindo que a variabilidade do salário seja a mesma nas duas cidades e que o modelo Normal é adequado, verifique se a cidade B paga, em média, melhor do que a cidade A. Obtenha o nível descritivo e tome sua decisão utilizando um nível de significância
Passo 1
Fala ai meu querido, vamos resolver essa questão rapidinho, ok? Trata-se de uma questão que se encaixa no 3A da seção 9.2 desse capítulo, e vou usar uma planilha de Excel com a ferramenta “Análise de Dados” ativada.
Passo 2
A ferramenta análise de dados possui uma função chamda “Teste-t: duas amostras presumindo variâncias equivalentes” que nos provêm os seguintes valores para essas amostragens:
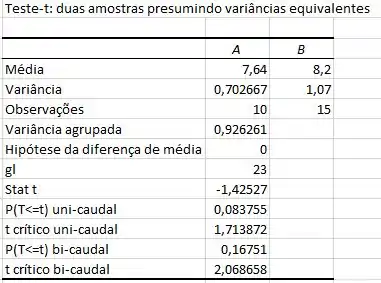
Passo 3
Nosso teste de hipótese é:
Temos um teste uni-caudal e precisamos calcular nosso :
Sendo:
Calculando esses valores, você irá encontrar:
Que é o valor que o Excel chama de Stat t.
Passo 4
Com , temos que nossa região crítica é , como nosso está dentro da área de aceitação, e podemos afirmar que não existe diferença entre a diferença média entre os salários pagos nas cidades A e B.
Resposta
Ei, a resposta está no passo a passo :)