Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 9.Exercícios - Ex. 93
Uma companhia opera quatro máquinas com três mudanças todo dia. Dos registros de produção, são coletados os seguinte dados do número de interrupções:
Teste a hipótese (usando alpha=0.05) de que as interrupções são independentes da mudança. Encontre o valor P para esse teste.
Passo 1
Determine as frequências observadas (O):
As frequências esperadas E são o produto do total da coluna e da linha, dividido pelo tamanho da amostra de n.
Os subtotais do qui-quadrado são as diferenças quadradas entre os observados e frequências esperadas, dividido pela frequência esperada.
Passo 2
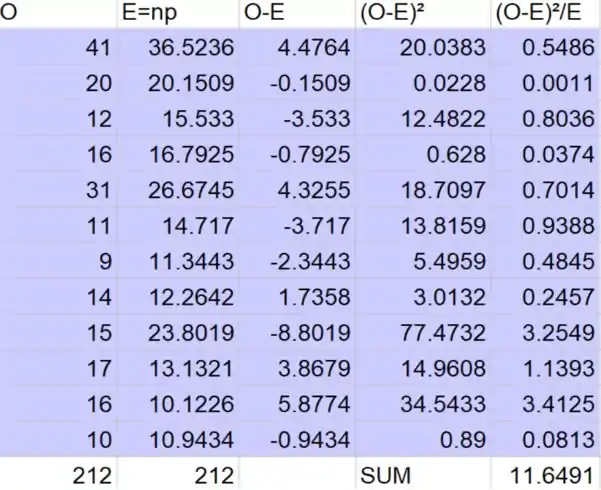
Passo 3
O valor da estatística de teste é então a soma dos subtotais qui-quadrado:
O valor P é a probabilidade de obter o valor da estatística de teste, ou um valor mais extremo. O valor P é o número (ou intervalo) na coluna Título da Tabela IV contendo o valor na linha
Se o valor P for menor ou igual ao nível de significância, então o valor da hipótese nula é rejeitada:
Não há evidências suficientes para rejeitar a reivindicação de independência.
Resposta
Não há evidências suficientes para rejeitar a reivindicação de independência.