Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Meyer - Aplicações a Estatística- Ed: 2º - Capítulo 3.Problemas - Ex. 21g

Duas máquinas A e B, sendo operadas independentemente, podem ter alguns desarranjos cada dia. A Tab. 3.2 dá a distribuição de probabilidades dos desarranjos· para cada máquina. Calcule as seguintes probabilidades:

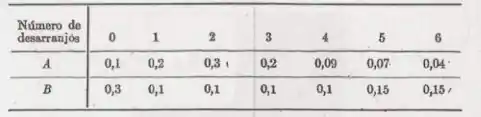
O número máximo de desarranjos das máquinas seja 3; seja maior que 3.

Passo 1

Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para encontrarmos a probabilidade desses eventos. Parece muita coisa, mas é tranquilo. Partiu??

Passo 2

Ok, nosso primeiro passo vai ser relembrar o que o exercício nos deu. Preparado??

A = i   d e s a r r a n j o s   n a   m á q u i n a   A

B = { i   d e s a r r a n j o s   n a   m á q u i n a   B }

E = i   d e s a r r a n j o s   n a   m á q u i n a   A   e   i   n a   m á q u i n a   B

Com esses valores, sabemos que podemos criar um espaço amostral com todas as possibilidades entre esses números.Dessa forma, podemos escrever do seguinte jeito:

X , Y = X 1 ,   Y 1 , X 1 ,   Y 2 , … ,   X n ,   Y n

P A ∪ B ∪ C   = P A + P B + P C - P A ∩ B - P A ∩ C - P B ∩ C + P A ∩ B ∩ C

Substituindo a relação na probabilidade, temos que:

P A i + B 1 > 3 = 1 - P ( A i + B 1 ≤ 3 )    

A i + B 1 < 3

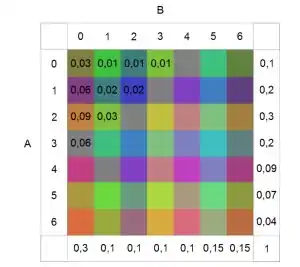
Passo 3

Pronto!! Agora é só obter nossa distribuição!!

P A i + B 1 > 3 = 1 - 0 , 34

P A i + B 1 > 3 =   0,66

Resposta

P A i + B 1 > 3 =   0,66

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Suponha que um equipamento possua N válvulas, todas necessárias para o seu funcionamento. A fim de localizar uma válvula com mau funcionamento, faz-se a substituição de cada válvula, sucessivamente, p
Três jornais A, B e C são publicados em uma cidade e uma recente pesquisa entre os leitores indica o seguinte: 20 por cento lêem A; 26 por cento lêem B; 14 por cento lêem C; 8 por cento lêem A e B; 5
Uma moeda equilibrada é jogada 2 n vezes.a) Obtenha a probabilidade de que ocorrerá um igual número de caras e coroas;b) Mostre que a probabilidade calculada em (a) é uma função decrescente de n .
Duas máquinas A e B, sendo operadas independentemente, podem ter alguns desarranjos cada dia. A Tab. 3.2 dá a distribuição de probabilidades dos desarranjos· para cada máquina. Calcule as seguintes pr
Duas máquinas A e B, sendo operadas independentemente, podem ter alguns desarranjos cada dia. A Tab. 3.2 dá a distribuição de probabilidades dos desarranjos· para cada máquina. Calcule as seguintes pr