Enunciado
Probabilidade e Estatística - Meyer - Aplicações a Estatística- Ed: 2º - Capítulo 3.Problemas - Ex. 35
Três jornais A, B e C são publicados em uma cidade e uma recente pesquisa entre os leitores indica o seguinte: 20 por cento lêem A; 26 por cento lêem B; 14 por cento lêem C; 8 por cento lêem A e B; 5 por cento lêem A e C; 2 por cento lêem A, B e C; e 4 por cento lêem B e C. Para um adulto escolhido ao acaso, calcule a probabilidade de que:
a) ele não leia qualquer dos jornais.
b) ele leia exatamente um dos jornais.
c) ele leia ao menos A e B, se se souber que ele lê ao menos um dos jornais publicados.
Passo 1
O enunciado apresenta um erro: ao invés de 40 por cento lêem B e C devemos considerar apenas 4 por cento!
O primeiro passo nesse tipo de problema é construir o diagrama de Venn:
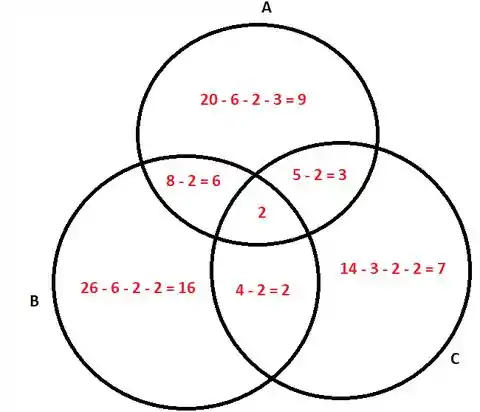
Note que nós partimos sempre do centro: como 8 lêem os jornais A e B e 2 lêem os três jornais, lêem apenas A e B, sem ler C. Seguindo o mesmo procedimento achamos o resto.
Observe que somando todas as porcentagens:
Logo, das pessoas lêem um desses jornais, de modo que não lê nenhum jornal. Isso responde o item (a):
Passo 2
Para achar a probabilidade de a pessoa ler exatamente um jornal, temos que somar:
Portanto,
Passo 3
Para que ele leia ao menos A ou B, temos que somar todos os casos em que a pessoa lê ao menos um desses jornais:
Como queremos a probabilidade sabendo que a pessoa lê pelo menos um desses jornais, nosso espaço amostral não é mais , ele passa a ser :