Exercícios de Teorema da Probabilidade Total - Lista de Exercícios Resolvida

Os colégios A, B e C têm as seguintes porcentagens de rapazes, respectivamente: 40%, 20% e 10%. Um desses colégios é selecionado ao acaso e oito alunos são escolhidos, com reposição. Se o resultado for RRRMMMMM (R para rapaz e M para moça), qual é a probabilidade de ter sido selecionado o colégio C?

Cada uma de 3 caixas possui 2 gavetas. A primeira caixa contém uma moeda de ouro em cada gaveta, a segunda caixa contém 2 moedas de prata em cada gaveta, e a terceira caixa, uma moeda de ouro em uma gaveta, e uma de prata na outra. Uma caixa é escolhida ao acaso; uma de suas gavetas é escolhida ao acaso e aberta, encontrando-se uma moeda de ouro. Qual a probabilidade que a moeda da outra gaveta seja também de ouro?

Para competir em uma certa regata as embarcações podem velejar com no máximo 4 tripulantes. Os tripulantes de cada embarcação são inscritos previamente e não podem ser alterados mais tarde. A embarcação Chez Moi, participante da regata, inscreveu Alberto, Bernardo, Carlos e Diogo. Carlos e Diogo confirmaram a presença na regata com probabilidade 100%. A probabilidade de Alberto comparecer à regata é 50%, enquanto que a de Bernardo, é 70%. A decisão de comparecer ou não por parte de Alberto não influencia a decisão de comparecer ou não por parte de Bernardo e vice versa. Note que o fato do número de velejadores no barco poder ser igual a 2, 3 ou 4 caracteriza uma partição do espaço amostral. Com a tripulação completa, a embarcação Chez Moi tem 80% de probabilidade de vencer a regata; com apenas Carlos e Diogo, esta probabilidade cai para 20%; e com três tripulantes a probabilidade de vencer é de 50%. Pede-se calcular a probabilidade de que:

1. pelo menos um dos velejadores, Alberto ou Bernardo, compareçam à regata;
2. a embarcação Chez Moi vença a regata;
3. pelo menos um dos velejadores, Alberto ou Bernardo, tenham comparecido à regata condicionado ao fato de que a embarcação Chez Moi venceu a regata. Compare suas respostas dadas nos itens (b) e (c). A probabilidade aumentou ou diminuiu? Por que?

Um modelo de motor é fabricado por 3 fábricas: A, B e C. Sabe-se que A produz o dobro de motores que B e que B e C produzem o mesmo número de motores. Sabe-se ainda que 2% das dos motores produzidos por A e por B são defeituosos, enquanto que 4% dos produzidos por C são defeituosos. Todos os motores produzidos são misturados e colocados em um depósito. Se do depósito for retirada um motor ao acaso, qual a probabilidade de que ele seja defeituoso?

Três pesquisadores pensam, de forma independente, na solução de um problema. Pela experiência e conhecimento de cada pesquisador sabe-se que as probabilidades de encontrar a solução são de para A, de para B e de para C . Calcule a probabilidade:

1. de que o problema seja resolvido;
2. de pelo menos dois dos três pesquisadores resolverem o problema;
3. condicional de B resolver o problema dado que este foi resolvido por pelo menos dois pesquisadores.

Suponha que um posto de combustível recebe 20% de sua gasolina do distribuidor D1, 30% do distribuidor D2 e 50% do distribuidor D3. Sabe-se que: dado que a gasolina vem de D1, 20% do seu conteúdo é adulterado; dado que a gasolina vem de D3, 2% do seu conteúdo é adulterado. Sabe-se também que a probabilidade de uma amostra aleatória de gasolina do posto estar adulterada é de 6,5%. A probabilidade de uma amostra aleatória de gasolina do posto ser adulterada dado que é de D2 é:

Um aluno faz a P1 de Probabilidade que é composta de testes múltipla escolha. Suponha que para cada teste ele sabe a resposta ou “chuta” e escolhe uma opção aleatoriamente. Suponha ainda que se ele sabe a resposta, a probabilidade da resposta estar correta é 1, e se ele “chuta”, essa probabilidade é 1/5. Para tirar 5,0 ,os alunos precisam responder pelo menos 50% das perguntas corretamente. O aluno "estudou para tirar 5,0", ou seja, ele sabe a resposta de um teste com probabilidade 0,5. Dado que ele responde corretamente um teste, qual é a probabilidade de que ele realmente saiba a resposta?

Seja um experimento aleatório que consiste no lançamento de dois dados onde e representam, respectivamente, o número inscrito em cada dado. Considere os eventos:

Pede-se:

I)Os resultados dos eventos acima indicados.

II)As probabilidades:

Para estudar o comportamento do mercado de smartphones, as marcas foram divididas em três categorias: marca , marca e marca . Um estudo sobre os hábitos de mudança de marca por parte dos usuários mostrou que o seguinte quadro de probabilidades condicionais prevalece em qualquer momento no qual um usuário típico adquire um novo aparelho:

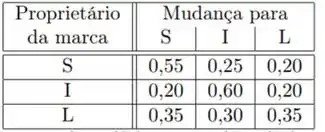
Por exemplo: Para . A compra do primeiro smartphone é feita conforme as probabilidades a seguir: . Calcule as probabilidades de um usuário:

(a) Comprar o seu segundo smartphone de cada uma das marcas: , e ;

(b) Comprar o seu terceiro smartphone da marca , ou seja, ;

(c) Ter comprado o seu primeiro smartphone da marca , dado que o segundo também foi da marca , ou seja,

Um jogo de futebol de video-game dispõe de nomes de jogadores da atualidade para compor o time da seleção brasileira. Esses jogadores são classificados como goleiros e não goleiros. Há goleiros e dentre eles está o Alisson e não goleiros e dentre estes está o Neymar. Sem levar em conta o time reserva, o game seleciona de forma aleatória primeiramente o goleiro e em seguida os outros jogadores. A probabilidade do time não conter o goleiro Alisson nem o Neymar vale:

2. ;
3. ;
4. ;
5. .

Para competir em uma certa regata as embarcações podem velejar com no máximo 4 tripulantes. Os tripulantes de cada embarcação são inscritos previamente e não podem ser alterados mais tarde. A embarcação Chez Moi, participante da regata, inscreveu Alberto, Bernardo, Carlos e Diogo. Carlos e Diogo confirmaram a presença na regata com probabilidade 100%. A probabilidade de Alberto comparecer à regata é 50%, enquanto que a de Bernardo, é 70%. A decisão de comparecer ou não por parte de Alberto não influencia a decisão de comparecer ou não por parte de Bernardo e vice versa. Note que o fato do número de velejadores no barco poder ser igual a 2, 3 ou 4 caracteriza uma partição do espaço amostral. Com a tripulação completa, a embarcação Chez Moi tem 80% de probabilidade de vencer a regata; com apenas Carlos e Diogo, esta probabilidade cai para 20%; e com três tripulantes a probabilidade de vencer é de 50%. Pede-se calcular a probabilidade de que:

1. pelo menos um dos velejadores, Alberto ou Bernardo, compareçam à regata;
2. a embarcação Chez Moi vença a regata;
3. pelo menos um dos velejadores, Alberto ou Bernardo, tenham comparecido à regata condicionado ao fato de que a embarcação Chez Moi venceu a regata. Compare suas respostas dadas nos itens (a) e (b). A probabilidade aumentou ou diminuiu? Por que?

O receptor de um determinado equipamento de uma rede de telecomunicações recebe mensagens de instruções através de um dentro três possíveis transmissores diferentes. Estatísticas da rede mostram que 50% das mensagens recebidas são enviadas pelo transmissor 1, 40% pelo transmissor 2 e 10% pelo transmissor 3. Para fins de garantia de integridade das informações, o protocolo de comunicação exige que o receptor confirme o recebimento repetindo ao seu transmissor a mensagem recebida. Entretanto, a chance dos transmissores enviarem mensagens contendo erros nos bits que os identificam é de 1%, 3% e 6%, respectivamente. Com base nessas estatísticas, calcule:

1. A probabilidade de chegar uma mensagem no receptor com erro na identificação do remetente e, portanto, o receptor não ter certeza sobre qual transmissor ele deve responder.
2. Para cada um dos três transmissores, a probabilidade deste ter sido o remetente de uma mensagem que chegou no receptor com erro na identificação.

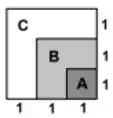
Um terreno quadrado de área apresenta três tipos de solo: , e , de acordo com a ilustração abaixo. Sabe-se que a chance de uma semente conseguir germinar no solo é , no solo é de e no solo é 20%. Além disso, assuma que a probabilidade de que uma semente levada pelo vento até esse terreno caia em cada um dos tipos de solo é proporcional a sua área.

1. Calcule a probabilidade de que um semente que caia nesse terreno consiga germinar.
2. Considerando que duas sementes caiam nesse terreno (de forma independente), calcule a probabilidade de que elas caiam em solos tipos diferentes.
3. Considere agora que as duas sementes caíram no mesmo tipo de solo e que, posteriormente, observou-se que ambas conseguiram germinar. Calcule qual a probabilidade de que o solo em que elas caíram seja do tipo A.

A temperatura de uma dada reação química é uma variável aleatória, cuja função densidade de probabilidade assume a forma

sendo a e b constantes reais. Depois de realizar vários experimentos, constatou-se que . Neste caso, os valores de a e b são respectivamente iguais a

1. ;
2. ;
3. ;
4. ;
5. .

O funcionamento do sistema ilustrado abaixo depende de 5 componentes: . Cada um desses componentes tem probabilidade 0,1 de estar defeituoso, independente dos demais; e o sistema irá funcionar apenas se houver pelo menos um caminho conectando os pontos A e B ao longo do qual nenhum componente esteja defeituoso.

a) Calcule a probabilidade de que pelo menos um dos 5 componentes esteja defeituoso.

b) Calcule a probabilidade desse sistema funcionar.

c) Calcule a probabilida de que o componente esteja defeituoso, dado que o sistema está funcionando.

Uma fábrica de televisores compra 1/5 de transistores que necessita de um fornecedor que garante uma confiabilidade (probabilidade de funcionar corretamente sem defeitos) de 80% ao seu material durante um certo período. A aquisição do restante material é igualmente dividida por duas outras firmas que garantem, respectivamente, confiabilidades de 85% e 95% durante o mesmo período de tempo.

a) Seleciona-se ao acaso um transistor do estoque da fábrica para teste. Qual a probabilidade dele funcionar corretamente?

Observação: mostre os resultados considerando 4 casas decimais.