Enunciado
Probabilidade e Estatística - Estatistica Mauri Guerra estatistica indutiva- Ed: 1º - Capítulo 1.Exercícios propostos - Ex. 2
Duas pessoas atiram numa caça; sabe-se que a probabilidade da 1ª pessoa acertar é 40% e da 2ª acertar 70%. Qual a probabilidade:
- de ambas acertarem;
- da caça ser atingida;
- de só uma acertar;
- de nenhuma acertar.
Passo 1
Olá galerinha, primeiramente vamos relembrar a definição de probabilidade.
Dada uma experiência aleatória qualquer, descrita num espaço de amostragem , chama-se probabilidade à função que, a cada evento , do espaço amostral , associa um número real, representado por , denominado probabilidade do evento , que satisfaz as seguintes propriedades:
- ;
- .
Então pelo enunciado, temos os seguintes dados:
evento do 1° atirador acertar o tiro:
evento do 2° atirador acertar o tiro:
No item (a) queremos saber a probabilidade de ambas as pessoas acertarem o tiro. Neste caso iremos utilizar a Regra do Produto para eventos independentes:
Passo 2
Já para a caça ser atingida, iremos utilizar o Teorema da Soma. Sendo e dois eventos quaisquer de um espaço amostral, então:
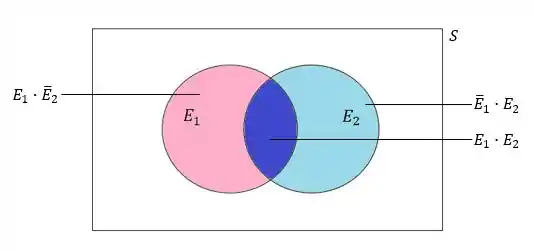
Onde a equação é:
O último item da equação, nós calculamos no Passo 1 (), então temos:
Passo 3
No item (c) queremos para acertar somente uma pessoa, para isso, sabemos que:
Onde:
Então teremos a seguinte equação:
Passo 4
No caso de nenhuma pessoa acertar, será o complemento () daquele que encontramos no Passo 1, iremos utilizar a seguinte equação:
Até mais pessoal!
Resposta
- ;
- ;
- ;
- .