Enunciado
Probabilidade e Estatística - Estatistica Mauri Guerra estatistica indutiva- Ed: 1º - Capítulo 1.Exercícios propostos - Ex. 15
Numa urna foram colocadas 5 bolas, de acordo com o seguinte esquema: joga-se 1 moeda, se sair cara coloca-se 1 bola branca, se sair coroa coloca-se 1 bola vermelha. Qual a probabilidade de que:
- a urna contenha exatamente 2 bolas brancas;
- a urna contenha exatamente 3 bolas brancas, com a condição que a 1ª bola colocada venha a ser branca.
- A urna contenha pelo menos 3 bolas brancas.
Passo 1
Olá galerinha, tudo bem com vocês? Vamos lá relembrar um pouco da teoria de probabilidade.
Dada uma experiência aleatória uniforme, definida num espaço de amostragem , define-se como probabilidade de ocorrer um evento , contido em , como sendo o quociente entre o número de elementos do evento e o número de elementos do espaço amostral , isto é, é o número de casos favoráveis ao evento, dividido pelo número total de casos possíveis.
Onde:
- número de elementos do evento ;
- número de elementos do espaço amostral .
E pelo enunciado, sabemos que:
- Cara (K) = bola branca;
- Coroa (C) = bola vermelha.
Como em cada lançamento há duas possibilidades (cara ou coroa), e teremos 5 lançamentos, o número de elementos no espaço amostral é:
Passo 2
No item (a) queremos que a urna tenha exatamente 2 bolas brancas, então precisamos que das 5 vezes em que a moeda for lançada, 2 vezes precisa ser cara, então temos as seguintes possibilidades:
Com isso, sabemos que . Sendo assim, a probabilidade de conter exatamente 2 bolas brancas na urna é:
Passo 3
No item (b) queremos que a urna contenha exatamente 3 bolas brancas, porém com a condição que a 1ª bola seja branca, então temos as possibilidades:
Com isso, sabemos que . Sendo assim, a probabilidade será:
Passo 4
No item (c) queremos que a urna contenha pelo menos 3 bolas brancas, então precisamos do número de possibilidades para 3, 4 e 5 bolas brancas, temos o seguinte:
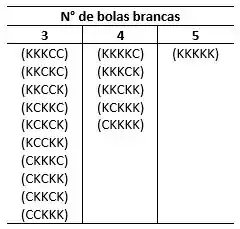
Então, para:
- 3 bolas brancas ;
- 4 bolas brancas ;
- 5 bolas brancas
A probabilidade de conter pelo menos 3 bolas brancas na urna é:
Consegui ajudar? Espero que sim! Até mais!
Resposta
- .
- .
- .