Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Walpole - Probabilidade e Estatística para Engenharia e Ciências- Ed: 8º - Capítulo 2.Exercícios - Ex. 134

Durante uma crise econômica, os funcionários de uma indústria são demitidos e substituídos por máquinas. O histórico de 100 trabalhadores que perderam o emprego devido aos avanços tecnológicos foi revisado. Para cada um desses indivíduos, foi determinado se ele recebeu um trabalho alternativo na mesma empresa; se encontrou um emprego em outra empresa, mas está trabalhando na mesma área; ou se está desempregado há um ano. Além disso, a situação sindical de cada um desses trabalhadores também foi registrada. A tabela abaixo sintetiza os resultados.

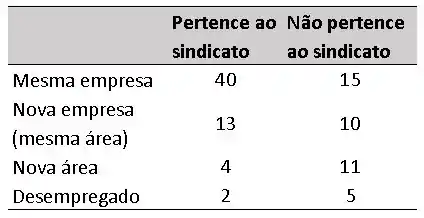
(a) Se um trabalhador selecionado encontrou trabalho na mesma área em outra empresa, qual é a probabilidade de que ele seja membro do sindicato?

(b) Se o trabalhador é membro do sindicato, qual é a probabilidade de que esteja desempregado há um ano?

Passo 1

Falaa, meu querido/minha querida. Abaixo podemos ver a tabela do enunciado melhor organizada, com somas totais já feitas.

Organizando os eventos:

Vamos usar M para representar o evento em que o funcionário trabalha na mesma empresa.

N para representar o evento no qual o trabalha em uma nova empresa.

F para o evento em que ele está em uma nova área.

D para o evento onde ele está desempregado.

Usaremos S para representar que pertence ao sindicato e S ' para não pertencente.

Então, bora lá resolver a questão!!

Passo 2

Queremos a probabilidade de que dado que funcionário encontrou trabalho na mesma área e em outra empresa, qual a chance de ele ser membro do sindicato. Então, precisamos achar P ( S | N ) .

Usando a definição da probabilidade condicional:

P S N = P ( S ∩ N ) P ( N )

Primeiro, vamos encontra P ( S ∩ N ) , pela tabela do passo 1:

P ( S ∩ N ) = n ú m e r o   d e   f u n c i o n á r i o s d o   s i n d i c a t o   q u e   a c h a r a m t r a b a l h o   e m   u m a   n o v a   e m p r e s a n a   m e s m a   á r e a t o t a l   d e   f u n c i o n á r i o s

P ( S ∩ N ) = 13 100

Agora, achando P ( N ) , também pela tabela:

P N = n ú m e r o   d e   f u n c i o n á r i o s q u e   a c h a r a m   t r a b a l h o e m   u m   n o v a   e m p r e s a   n a   m e s m a   á r e a t o t a l   d e   f u n c i o n á r i o s

P N = 23 100

Sendo assim, P ( S | N ) é definido por:

P S N = P ( S ∩ N ) P ( N ) = 13 100 23 100 = 13 23 = 0,565

Passo 3

Queremos a probabilidade de que dado que funcionário é do sindicato, qual a chance de estar desempregado há 1 ano. Então, precisamos achar P ( D | S ) .

Usando a definição da probabilidade condicional:

P D S = P ( D ∩ S ) P ( S )

Primeiro, vamos encontra P ( D ∩ S ) , pela tabela do passo 1:

P ( D ∩ S ) = n ú m e r o   d e   f u n c i o n á r i o s d o   s i n d i c a t o   d e s e m p r e g a d o s h á   1   a n o t o t a l   d e   f u n c i o n á r i o s

P ( D ∩ S ) = 2 100

Agora, achando P ( S ) , também pela tabela:

P S = n ú m e r o   d e   f u n c i o n á r i o s d o   s i n d i c a t o t o t a l   d e   f u n c i o n á r i o s

P S = 59 100

Portanto, P ( D | S ) é definido por:

P D S = P ( D ∩ S ) P ( S ) = 2 100 59 100 = 2 59 = 0 , 034

Resposta

a) 0,565

b) 0,034

Exercícios de Livros Relacionados

Dizemos que A ⊂ B (A é subconjunto de B) se todo elemento de A também pertence a B. Por exemplo, {1, 2} ⊂ {1, 2, 3}. Se P(A) = 1/3, P(Bc) = 1/4, A e B podem ser disjuntos (ou mutuamente exclusivos)?
A probabilidade de que um veículo entrando nas cavernas Luray tenha placa canadense é de 0,12; a probabilidade de que seja um trailer é de 0,28; e a probabilidade de ser um trailer com placa canadense
Qual é probabilidade de que dois estudantes não tenham a mesma data de nascimento em uma classe com 60 alunos? (Veja o Exercício 2.50.)
Há uma chance de 50% de que uma rainha carregue o gene da hemofilia. Se ela for portadora do gene, então cada príncipe terá, independentemente, 50% de chance de ter hemofilia. Se a rainha não for port