Enunciado
Probabilidade e Estatística - Estatistica Mauri Guerra estatistica indutiva- Ed: 1º - Capítulo 2.Exercícios propostos - Ex. 4
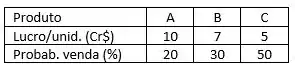
Uma empresa vende três produtos cujos lucros e probabilidades de venda estão anotados na tabela. Calcular:
- O lucro médio por unidade vendida, bem como o desvio padrão;
- O lucro total esperado, num mês em que foram vendidas 2000 unidades.
Passo 1
Olá galerinha, tudo bem com vocês? Então vamos lá!
Relembrando que uma variável aleatória é sempre associada a seus resultados mutuamente exclusivos a probabilidade. E a variável aleatória é dita discreta quando pode assumir um número finito de valores dentro de um intervalo finito.
A distribuição de probabilidades é uma série de eventos mutuamente exclusivos que constituem a totalidade dos resultados numa experiência aleatória, isto é:
A cada evento , associamos um número real , e teremos como consequência que:
Passo 2
Então, vamos lá para o nosso exercício. Considerando que:
- N° de chamadas/dia;
- % dias.
E sabendo que a média de distribuição (), da variável , é a soma dos produtos dos valores da variável pelas respectivas probabilidades, isto é:
E o desvio padrão pela seguinte equação:
Rearranjando a tabela:
Passo 3
Então iremos calcular o valor de para cada :
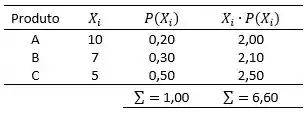
Então a média de distribuição é:
Com o valor da média conseguimos calcular o desvio padrão:
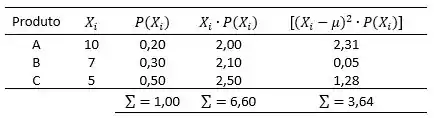
Então:
Passo 4
No item (b) queremos descobrir o lucro total esperado em um mês que foram vendidas 2000 unidades. E já sabemos que a média é . Então teremos:
Prontinho galerinha, espero ter ajudado!
Resposta
- ;
- .
.