Enunciado
Probabilidade e Estatística - Estatística Aplicada Farber e Larson- Ed: 6º - Capítulo 4.1 - Ex. 34
Encontrando a média, a variância e o desvio padrão. Nos exercícios 29 a 34, (a) encontre a média, a variância e o desvio padrão da distribuição de probabilidade e (b) interprete os resultados.
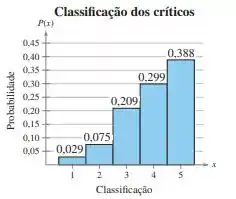
34. Classificação dos críticos O histograma da figura a seguir mostra a classificação dos críticos, em uma escala de 1 (mais baixo) a 5 (mais alto), de um produto em um site de varejo.
Passo 1
Fala galerinha boa, tudo bem? Vamos para mais uma questão de distribuição de probabilidades. Para calcular a média devemos usar a fórmula do valor esperado em probabilidades:
Onde x será o valor dado na distribuição e o valor de cada probabilidade associada a x.
Passo 2
Deste modo, basta substituir os valores na fórmula para encontra a média:
O número médio de cachorros por domicílio é de 3,942.
Passo 3
Para calcular a variância, usaremos a seguinte fórmula:
Onde:
Onde novamente x será o valor dado na distribuição e o valor de cada probabilidade associada a x.
Passo 4
Para encontrar a variância vamos fazer primeiramente :
E assim, podemos substituir os valores na fórmula da variância:
A variância é 1,155.
Passo 5
Para encontrar o desvio padrão, basta fazer a raiz da variância.
O desvio padrão da distribuição é ±1,075.
E é isso galera, questão um pouco maior, mas que busca todos os parâmetros da distribuição de probabilidades. Até a próxima!
Resposta
A média é aproximadamente 4, então a classificação dos críticos de um produto em um site de varejo gira em torno da nota 4. O desvio padrão é 1,0, então a maioria das classificações difere da média por não mais que 1 nível de classificação.