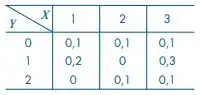
A tabela abaixo dá a distribuição conjunta de X e Y.
(a) Determine as distribuições marginais de X e Y.
(b) Obtenha as esperanças e variâncias de X e Y.
(c) Verifique se X e Y são independentes.
(d) Calcule e .
(e) Calcule e .
Passo 1
(a) Determine as distribuições marginais de X e Y.
Vamos lá!
Da tabela do enunciado podemos obter facilmente as distribuições de X e Y. A primeira e última colunas da tabela dão a distribuição de Y, (y, p(y)), enquanto a primeira e última linhas da tabela dão a distribuição de X, (x, p(x)). Essas distribuições são chamadas DISTRIBUIÇÕES MARGINAIS.
Vamos fazer alguns exemplos?
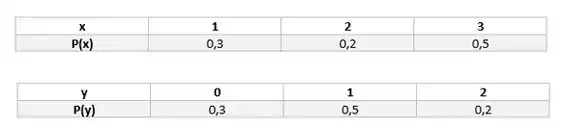
Seguindo esse raciocínio, podemos montar as nossas tabelas das distribuições marginas de X e Y.

![]()
Passo 2
(b) Obtenha as esperanças e variâncias de X e Y.
Sabemos que
Portanto
Para o cálculo da precisamos lembrar da seguinte fórmula:
Portanto, precisamos calcular e
Substituindo nas fórmulas, temos:
Passo 3
(c) Verifique se X e Y são independentes.
Não, pois
Passo 4
(d) Calcule e .
Para calcularmos a condicional, precisamos lembrar da fórmula da probabilidade. Vamos lembrar juntos?
Bom, sabemos na tabela que as probabilidades marginais representam a probabilidade de cada variáveil aleatória em um certo ponto, enquanto os outros componentes das tabelas são as probabilidades conjuntas, da interseção.
Quando a questão pede a distribuição condicional de X, dado que Y=0, queremos:
Partiu para as contas então?
Olhando para a tabela, sabemos que , portanto
Olhando para a tabela, sabemos que , portanto
Passo 5
(e) Calcule e .
Primeira coisa que devemos olhar são quais eventos estão aí dentro:
-
Então queremos
Logo, olhando para a tabela
Resposta
(a)
(b)
(c) Não, pois
(d)
(e)