Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 12.Exercícios - Ex. 25
Mostre que b1 e b0 das expressões (12.2) e (12.3) satisfazem as equações normais
Passo 1
A estimativa de mínimos quadrados da inclinação é
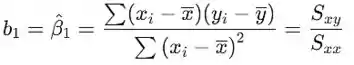
onde pode ser calculado pela fórmula
e pode ser calculado pela fórmula
A equação normal é
Ao substituir e na primeira equação você obtém
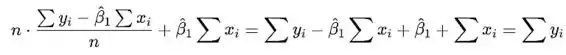
Passo 2
o que prova que as estimativas satisfazem a primeira equação. Substitua, novamente do lado esquerdo, e na segunda equação
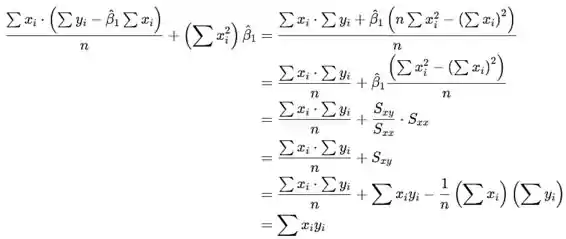
o que prova que as estimativas satisfazem a segunda equação.
Resposta
Substitua a estimativa de mínimos quadrados em equações normais para provar a afirmação
Exercícios de Livros Relacionados
Uma empresa produtora de cimento, desejando abrir uma fábrica no Paraná, realizou um estudo da demanda do produto, com a finalidade de pleitar um empréstimo junto ao BNDE. Para isto, coletou dados sob
Em uma avaliação de cargos, pelo método dos pontos, o salário ( Y ), expresso em Cr$ 100,00, está relacionado com o nível de instrução ( X 1 ) e com o nível de supervisão ( X 2 ) pela fórmula: Y = a +
Foi feito o levantamento, com n = 12 pessoas, a respeito da idade Y , em função da respectiva altura X 1 (em cm) e do respectivo peso X 2 (em kg).Efetuando os cálculos dos somatórios necessários à mon
Uma empresa produz sapatos do tipo popular, numa quantidade anual vendida Y (em mil unidades). Pretende-se verificar a relação entre essa quantidade vendida e o preço relativo da única concorrente exi
Uma empresa produz sapatos do tipo popular, numa quantidade anual vendida Y (em mil unidades). Pretende-se verificar a relação entre essa quantidade vendida e o preço relativo da única concorrente exi