Enunciado
Probabilidade e Estatística - Estatistica Mauri Guerra estatistica indutiva- Ed: 1º - Capítulo 14.Exercícios propostos - Ex. 9c
Foi feito o levantamento, com pessoas, a respeito da idade , em função da respectiva altura (em cm) e do respectivo peso (em kg).
Efetuando os cálculos dos somatórios necessários à montagem de regressão, obtivemos:
Pede-se:
- Interpretar os valores dos parâmetros da regressão múltipla.
Passo 1
Olá galerinha, tudo bem com vocês? Primeiramente iremos relembrar a teoria.
A regressão linear múltipla é a regressão em que sabemos como variáveis contribuem para a realização do fenômeno, e a parte funcional da regressão é uma função linear. Onde a estimativa da equação de regressão é dada por:
Onde as estimativas , , , , dos coeficientes , , , , podem ser calculadas pelo método dos mínimos quadrados, partindo de hipóteses análogas aquelas adotadas pela regressão linear simples.
Para o caso de ter apenas duas variáveis explicativas:
Para encontrarmos os valores de , e , iremos utilizar as equações:
Onde iremos precisar calcular aas médias (, e ) pelas seguintes equações:
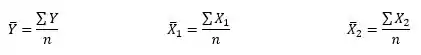
As variâncias vamos usar as equações:
E as covariâncias:
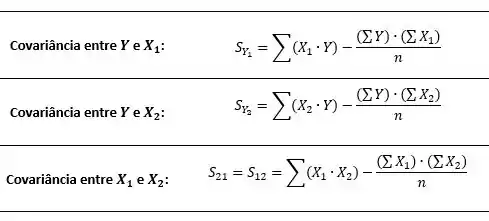
Passo 2
Então vamos para o nosso exercício. Do enunciado temos os seguintes dados:
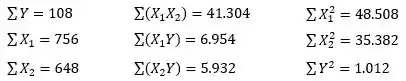
Primeiramente, vamos calcular as médias de , e , respectivamente:
Agora iremos calcular as variâncias:
E as covariâncias:
Passo 3
Com esses valores, finalmente conseguimos calcular os valores de , e :
Do enunciado sabemos que:
- idade;
- altura (em cm);
- peso (em kg).
Então, temos o seguinte:
- acréscimo na idade para cada 1 cm de altura;
- acréscimo da idade para cada 1 kg de peso.
Prontinho pessoal, até mais!
Resposta
Resposta no Passo 3.