Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 11.Problemas - Ex. 25

Estime o salário médio dos empregados de uma indústria têxtil, sabendo-se que uma amostra de 100 indivíduos apresentou os seguintes resultados:

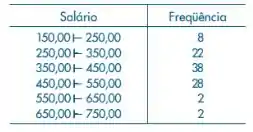
Use γ = 0,95.

Passo 1

Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para acharmos o IC da amostra para o estimador. Parece muita coisa, mas é tranquilo. Partiu??

Passo 2

Ok, nosso primeiro passo vai ser lembrar qual a fórmula do intervalo de confiança. Lembrou?? Então anota aí para mim...

I C μ ; γ =   X - z γ σ n   ;   X + z γ σ n    

e = z γ s n

Como já relembramos as fórmulas, vamos analisar os dados.

A média será dada como a média para dados agrupados que é:

x - = ∑ x i f n

Teremos então:

x - = 200 × 8 + 300 × 22 + 400 × 38 + 500 × 28 + 600 × 2 + 700 × 2 100

x - = 400

A variância amostral será:

σ = ∑ x i - x - 2 × f i n - 1

σ = ( ( 200 - 400 2 × 8 ) + 300 - 400 2 × 22 + 400 - 400 2 × 38 + 500 - 400 2 × 28 + 600 - 400 2 × 2 + 700 - 400 2 × 2 × 1 99

σ = 10909,1

s = 104,75

Sabendo esses parâmetros, agora faremos:

z 0,95 = 0,3894

z γ s n = 0,3894 × 104,75 100 = 4,08

Passo 3

Pronto!! Agora é só analisarmos!!

I C μ ; 0,95 =   ] 395,92   ;   4 04 , 08   [  

Resposta

I C μ ; 0,95 =   ] 395,92   ;   404,08   [  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

É importante que as máscaras usadas pelos bombeiros sejam capazes de resistir a altas temperaturas, pois esses profissionais trabalham com frequência em temperaturas de 200-500 F . Em um teste de um t
O gerente financeiro de uma grande rede de lojas de departamentos selecionou uma amostra aleatória de 200 de seus clientes com cartão de crédito e descobriu que 136 pagaram juros no ano anterior devid
Um triatlo que consiste em nadar, andar de bicicleta e correr é um dos eventos de esporte amador mais árduos. O artigo "Cardiovascular and Thermal Response of Triathlon Performance" (Medicine and Scie
O Exemplo 1.11 introduziu as observações que seguem sobre resistência de contato. 11,5 12,1 9,9 9,3 7,8 6,2 6,6 7,0 13,4 17,1 9,3 5,6 5,7 5,4 5,2 5,1 4,9 10,7 15,2 8,5 4,2 4,0 3,9 3,8 3,6 3,4 20,6 25,
Suponha que x 1 , x 2 , … , x n sejam valores observados que resultam de uma amostra aleatória de distribuição simétrica, porém possivelmente de cauda longa. Sejam x ˜ e f s a mediana da amostra e a q