Em um estudo sobre um novo método para ensinar Matemática a alunos do primeiro

grau, dez crianças foram selecionadas ao acaso de um grupo de e ensinadas pelo

novo método, enquanto as outras dez serviram como controle e ensinadas pelo método

tradicional. Após dez semanas o desempenho dos alunos em um teste foi avaliado e

obtiveram-se as seguintes notas:

Teste, com nível , a hipótese de que o novo método é mais eficaz, utilizando o

teste e o teste Wilcoxon. Obtenha em cada caso.

Vamos testar se as variâncias são homogêneas, ou seja:

Observe que:

Sob ,

Assim, a região crítica do teste, tomando é:

Como , não reijeitamos a hipótese de igualdade de variância.

Agora, vamos testar, através do teste de Student, se as médias são iguais:

Sob , .

Considerando , temos que .

Como , não há indícios para concluir que o novo método é mais eficaz.

Realizaremos agora o teste de Wilcoxon.

Primeiramente, vamos ordenar da menor para a maior, as observações obtidas no estudo, identificando os postos correspondentes a cada observação.

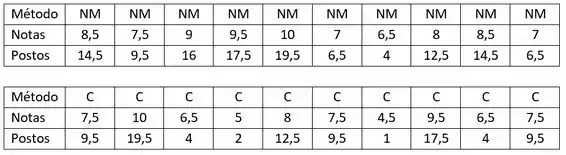
Observe que, no caso de observação coincidentes ou empates, foram considerados os postos médios.

Calculemos a estatística referente à soma dos postos das notas do novo método:

Para esta estatística, temos:

Vamos calcular a estatística do teste :

Sob , aproximadamente.

Considerando , temos que a região crítica do teste é dada por

Como , não há indícios para concluir que o novo método seja mais eficaz.