Enunciado
Probabilidade e Estatística - Estatística Aplicada Farber e Larson- Ed: 6º - Capítulo 4.1 - Ex. 23
Eventos incomuns. No Exercício 19, seria incomum para um domicílio não ter televisor? Explique seu raciocínio
Passo 1
A tabela de distribuição de probabilidades dada no exercício 19 é mostrada abaixo, onde X é a variável aleatória que determina a quantidade de televisores por domicílio e P(X) é a probabilidade associada.
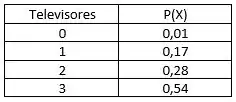
Passo 2
A tabela de distribuição de probabilidades mostra que a probabilidade de um domicílio não ter televisor é de 0,01 (1%). Deste modo, a probabilidade de um domicílio ter pelo menos um televisor é de 99%, sendo incomum não ter televisor em um domicílio.
Resposta
Sim, porque a probabilidade é menor que 0,05 (5%).
Exercícios de Livros Relacionados
Considere uma urna contendo três bolas vermelhas e cinco pretas. Retire três bolas, sem reposição, e defina a v.a. X igual ao número de bolas pretas. Obtenha a distribuição deX .
Repita o problema anterior, mas considerando extrações com reposição.
Para uma v.a. com distribuição qui-quadrado, com ν graus de liberdade e ν par, vale a seguinte fórmula: P χ 2 vc = e - c / 2 × ∑ j = 0 v 2 - 1 c 2 j j ! Calcule essa probabilidade para os seguintes ca
Usando a aproximação normal a uma variável qui-quadrado, calcular:(a) P ( χ 2( 35 )49,76 ) ;
Distribuição de Weibull. Um modelo que tem muitas aplicações na teoria da confiabilidade é o modelo de Weibull, cuja f.d.p. é dada por: f x = ∝ β x β - 1 e - α x β ,x ≥ 0 0 ,x0 , Onde α eβ são constan