Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 12.Exercícios - Ex. 68
12-68. O,dados mostrados a seguir foram coletados durante um expe-
rimento para determinar a variação na eficiência de impulsão (y. cm
porcentagem) à medida que varia o ângulo de divergencia de um bocal
de um fogucte (x):
a) Ajuste um modelo de segundo grau a esses dados.
b) Teste a significância da regressão c a falta de ajuste. usando a = 0.05.
c) Teste a hipotese de que ir - O usando a - 0,05.
d) Plote os residuos e comente a adequação do modelo.
e) Ajuste um modelo cúbico e teste a significância do termo cúbico
usando a = 0.05.
Passo 1
Faaaala ai gente, tudo bom?
Vamos resolver essa questão aqui rapidinho?
Bora, é tranquilo
Letra a:
Ajuste o modelo de regressão linear (neste caso - modelo polinomial de 2ª ordem) para obter:
Passo 2
Letra b:
A estatística de teste F deve ser calculada da seguinte maneira.
Nós sabemos que:
Vamos lembrar que:
Em seguida, calcule a partir dos dados:
Agora podemos calcular:
Portanto, a estatística F é
O valor P para o teste de significância da regressão é então obtido como
A hipótese é então rejeitada e a regressão é significativa
Passo 3
Letra c:
Lembre-se de como o teste F parcial é feito e o que isso significa.
Defina r=1 e
Então,
A estatística de teste F deve ser calculada da seguinte maneira.
Lembre-se que:
Então você tem que calcular (tendo em mente que esses números são obtidos a partir de modelos completamente diferentes!):
Portanto, a estatística F é
O valor P para o teste de significância da regressão é então obtido como
A hipótese
é, portanto, rejeitada, o que significa que a contribuição da variável é significativa para o modelo.
Passo 4
Letra d:
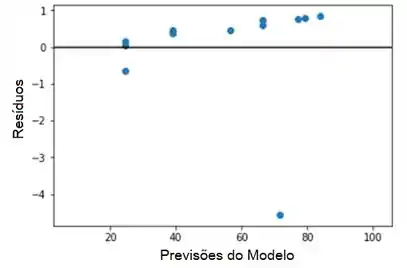
Plote os resíduos do modelo versus as previsões do modelo. O gráfico sugere que o modelo não é adequado. Quase todos os resíduos são colocados acima do eixo horizontal (y = 0).
Então,
A hipótese é, portanto, rejeitada e a regressão é significativa.
Passo 5
Letra e:
Agora ajuste o modelo cúbico aos dados. O melhor ajuste linear obtido é:
Lembre-se de como o teste F parcial é feito e o que isso significa. Agora aplicamos o teste F parcial (equivalente ao teste t) para o coeficiente cúbico do modelo.
Defina r=1 e
Então,
A estatística de teste F deve ser calculada da seguinte maneira.
Lembre-se que:
Então você tem que calcular (tendo em mente que esses números são obtidos a partir de modelos completamente diferentes!):
Portanto, a estatística F é
O valor P para o teste de significância da regressão é então obtido como
A hipótese
portanto, não pode ser rejeitada, o que significa que a contribuição da variável não é significativa para o modelo.
Resposta
- Ver resolução