Enunciado

Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 11.Exercícios - Ex. 3

artigo "Adiabatic Humidification of Air with Water in a Packed Tower" (Chem. Eng. Prog., 1952, p. 362370) apresenta dados sobre o coeficiente de condutividade térmica da película gasosa [Btu/(hr.pés )] como função da taxa de gás (fator ) e da taxa de líquido (fator ).

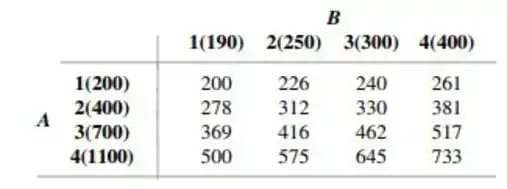
a. Depois de elaborar uma tabela ANOVA, teste, no nível 0,01 , tanto a hipótese de ausência de efeito da taxa de gás contra a alternativa apropriada, como a hipótese de ausência de efeito da taxa de líquido contra a alternativa apropriada.

b. Use o procedimento de Tukey para investigar diferenças no coeficiente de condutividade térmica esperado decorrentes de diferentes taxas de gás.

c. Repita a parte (b) para as taxas de líquido.

Passo 1

E aí pessoal partiu para mais uma questão de (probabilidade)? Abaixo começaremos trazendo algumas informações do enunciado:

a. Depois de elaborar uma tabela ANOVA, teste, no nível 0,01 , tanto a hipótese de ausência de efeito da taxa de gás contra a alternativa apropriada, como a hipótese de ausência de efeito da taxa de líquido contra a alternativa apropriada.

Agora sabendo o que o exercício pede na opção A vem cmg 😊

,,,

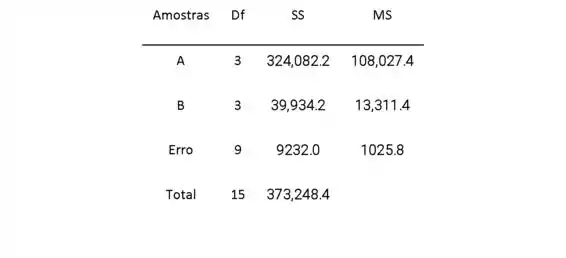
Uma vez que

Passo 2

Todos os níveis de Fator A (taxa de gás) diferem significativamente, exceto 1 e 2

Passo 3

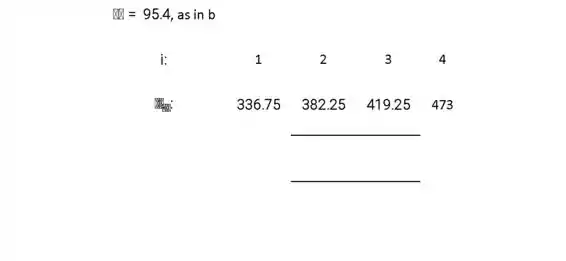
Apenas os níveis 1 e 4 parecem diferir significativamente.

Resposta

Uma vez que

b. Todos os níveis de Fator A (taxa de gás) diferem significativamente, exceto 1 e 2

c. Apenas os níveis 1 e 4 parecem diferir significativamente.

Espero que tenham aprendido com essa questão, até a próxima !

Exercícios de Livros Relacionados

a. Uma regressão linear poderia resultar nos resíduos 23, 27, 5, 17, 8, 9 e 15? Por quê? b. Uma regressão linear poderia resultar nos resíduos 23, 27, 5, 17, 8, 12 e 2 correspondentes aos valores x 3,

Lembre-se de que ˆ 0 ˆ 1x tem uma distribuição normal, com valor esperado 0 1x e variância de modo que tem uma distribuição normal padronizada. Se S SQE/(n2) for substituída por , a variável resultant

a. Expresse o i-ésimo resíduo Yi Yˆ i (onde Yˆ i ˆ 0 ˆ 1xi ) na forma cj Yj , uma função linear dos Yj s. Em seguida, use regras de variância para provar que V(Yi Yˆ i ) é dada pela Expressão (13.2).

Se houver pelo menos um valor x no qual foi feita mais de uma observação, existe um procedimento de teste formal para testarSuponha que se façam observações em x1, x2, ..., xc. Sejam Y11, Y12, ..., Y1

Os dados a seguir sobre a taxa de combustão de massa x e comprimento da chama y são representativos dos dados apresentados no artigo “Some Burning Characteristics of Filter Paper” (Combustion Science