Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 10.Exercícios Suplementares - Ex. 42
A frequência crítica de oscilação (fco) é a frequência mais alta (em ciclos/s) na qual uma pessoa pode detectar a oscilação em uma fonte de luz oscilante. Em frequências acima de fco, a fonte de luz parece ser contínua, embora na verdade esteja oscilante. Uma investigação realizada para verificar se a fco média real depende da cor da íris gerou os seguintes dados (com base no artigo "The Effects of Iris Color on Critical Flicker Frequency", J. General Psych., 1973, p. 91-95):
a. Expresse e teste as hipóteses de interesse no nível de significância 0,05 usando a tabela F para obter um limite superior e/ou inferior no valor P. (Sugestão: x2 ij 13.659,67 e OC 13.598,36.) b. Investigue as diferenças entre as cores da íris em relação à fco média
Passo 1
-
A tabela fornecida resume tudo o que você precisa para testar as hipóteses relevantes.
As hipóteses de interesse são
versus hipótese alternativa
é a verdadeira média de CFF para 3 cores, .
Tamanhos de amostra desiguais
Seja sejam os tamanhos de amostra dos tratamentos e sejam ser o número total de observações. Denote com
A soma total dos quadrados (SST), tratamento soma de quadrados (SSTr), e erro soma dos quadrados (SSE) são dados por
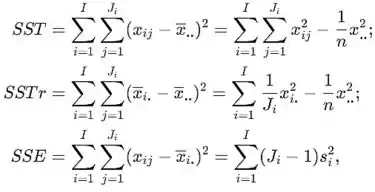
Com os graus de liberdade, respectivamente
Passo 2
A identidade fundamental:
Os quadrados médios são
F é a razão dos dois quadrados médios
O valor P é a área sob o curva à direita de f. Os graus de liberdade são, para n=133
A soma dos quadrados do tratamento é
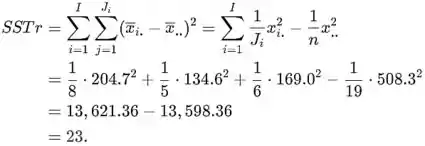
A soma total dos quadrados é
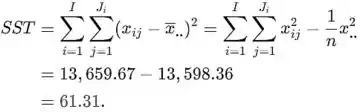
Pela identidade fundamental, vale o seguinte
Passo 3
Os quadrados médios são
F é a razão dos dois quadrados médios
O valor PP é a área sob o curva para a direita de f
que foi computado por meio de um software; você pode estimar o valor usando a tabela no apêndice. O seguinte vale
Então rejeitar hipótese nula em dado nível significativo (0.05). Além disso, se você usou o valor P, porque
rejeitar hipótese nula em determinado nível significativo. A conclusão é que há diferença significativa nas médias verdadeiras para os três tratamentos.
- Denote com
então a probabilidade de
é aproximadamente para todo e todo onde .
Da tabela no apêndice, para , e , vale o seguinte
Usando o método de Turkey modificado para obter os intervalos de confiança para cada par, você pode concluir as diferenças entre as cores da íris.
Dadas as médias e , os intervalos de confiança podem ser calculados usando a fórmula
Calculando primeiro
Onde MSE pode ser calculado em (a) e
Assim, os intervalos são
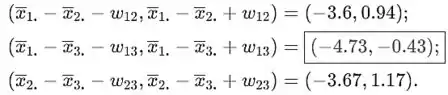
Como apenas o intervalo para o par (2,3)(2,3) não inclui zero, pode-se concluir que há diferença estatística apenas entre CFF para a cor marrom e azul
Resposta
- Rejeitar hipótese nula;
- Diferente para a cor da íris marrom e azul.