Explique, com suas palavras, por que, na regra da adição, para P(A ou B ou C), P(A e B e C) é somado ao final da fórmula.

Salve, fera! Tudo bem? Vamos encarar essa questão! Ela precisa de um pouco de interpretação, mas conseguimos entender ela sim.

Quando temos a probabilidade da união de dois eventos, dada por:

P(A ou B) = P(A) + P(B) − P(A e B)

Representada pelo diagrama a seguir:

Podemos analisar e entender o motivo pelo qual devemos descontar o valor da interseção entre A e B para calcular sua probabilidade. De forma rápida, se formos somar a probabilidade de cada um separadamente, estaríamos realizando a soma da região de interseção duas vezes, por isso devemos descontar uma delas para que a probabilidade indique o seu valor exato.

Para a união de três conjuntos, por definição, temos que:

P(A ou B ou C) = P(A) + P(B) + P(C) − P(A e B) − P(A e C) − P(B e C) + P(A e B e C).

Representada pelo diagrama a seguir:

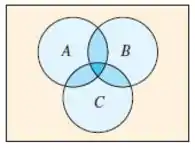
Seguindo o mesmo raciocínio anterior, vemos que estaríamos somando duas vezes as regiões de interseção entre duas regiões, porém ao retirá-las, descartamos também a região de interseção entre os três conjuntos. Deste modo, devemos somá-la para obter a probabilidade correta.

Espero ter ajudado! Abraços e até a próxima!