Enunciado
Probabilidade e Estatística - Estatística Aplicada Farber e Larson- Ed: 6º - Capítulo 3.3 - Ex. 28
No diagrama de Venn, a seguir, P(A ou B ou C) é representado pelas áreas em azul. Nos exercícios 28 e 29, encontre P(A ou B ou C).
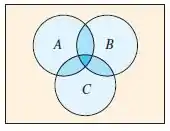
P(A) = 0,40, P(B) = 0,10, P(C) = 0,50,
P(A e B) = 0,05, P(A e C) = 0,25, P(B e C) = 0,10,
P(A e B e C) = 0,03.
Passo 1
Salve, fera! Tudo bem? Vamos encarar essa questão! Ela é bem simples.
Por definição, temos que:
P(A ou B ou C) = P(A) + P(B) + P(C) − P(A e B) − P(A e C) − P(B e C) + P(A e B e C).
Como o enunciado já deu todas as probabilidades ficou molezinha. É só substituir, assim:
P(A ou B ou C) = 0,40 + 0,10 + 0,50 – 0,05 – 0,25 – 0,10 + 0,03 = 0,57
Espero ter ajudado! Abraços e até a próxima!
Resposta
P(A ou B ou C) = 0,57.
Exercícios de Livros Relacionados
Um dado é lançado e, independentemente, uma carta é extraída de baralho completo (52 cartas). Qual será a probabilidade de que: a O dado mostre um número par e a carta seja de um naipe vermelho? b O d
Sejam A e B dois eventos associados um experimento. Suponha que P A = 0,4 , enquanto P A ∪ B = 0,7 . Seja P B = p . ( a ) Para que valor de p , A e B serão mutuamente excludentes? b Para que valor de
Se P ( A | B ) = 0.3 ,P ( B ) = 0.8eP ( A ) = 0.3 , o evento B e o evento complementar de A são independentes?
Se P ( A | B ) = 0.3 , P ( B ) = 0.8 e P ( A ) = 0.5 , os eventos A e B são independentes?
2-112. Um cartão de crédito contém 16 dígitos. Ele contém também um mês e ano de expiração. Suponha que haja um milhão de usuários de cartão de crédito com números únicos de cartão. Um invasor selecio