Enunciado
Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 9.Problemas - Ex. 29
Um florista faz estoque de uma flor de curta duração que lhe custa $0,50 e que ele vende a $1,50 no primeiro dia em que a flor está na loja. Toda flor que não é vendida nesse primeiro dia não serve mais e é jogada fora. Seja X a variável aleatória que denota o número de flores que os fregueses compram em um dia casualmente escolhido. O florista descobriu que a função de probabilidade de X é dada pela tabela abaixo.
Quantas flores deveria o florista ter em estoque a fim de maximizar a média (valor esperado) do seu lucro?
Passo 1
O florista pode ter em seu estoque 1, 2 ou 3 flores. Vamos chamar de L o lucro obtido. E calcular esse lucro para cada hipótese da quantidade de flores no estoque.
Lembrando da fórmula do valor esperado
Passo 2
Uma flor:
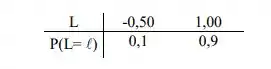
Passo 3
Duas flores:
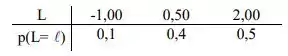
Passo 4
Três flores:
Resposta
Portanto, o estoque que maximiza o lucro médio é de 2 flores.