Enunciado

Probabilidade e Estatística - Estatística Aplicada Farber e Larson- Ed: 6º - Capítulo 2.4 - Ex. 49

Fórmula abreviada - Você usava quando calculava a variância e o desvio padrão da amostra. Uma fórmula alternativa que, às vezes, pode ser mais conveniente para cálculos à mão é:

Você pode encontrar a variância amostral dividindo a soma dos quadrados por n – 1 e o desvio padrão amostral encontrando a raiz quadrada da variância amostral.

(a) Use a fórmula abreviada para calcular o desvio padrão amostral para os dados do Exercício 15.

(b) Compare seus resultados com os obtidos no Exercício 15

Passo 1

Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!

Notamos que o conjunto de dados contém 20 valores, portanto

Fazendo uma tabela, nós temos que

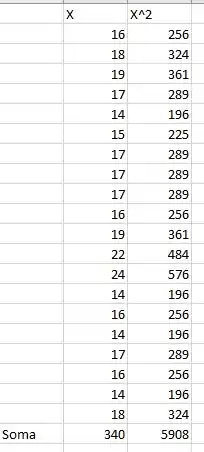
Passo 2

Usando a fórmula de atalho, obtemos:

Substituindo os valores, nós temos que

O que nos fornece o seguinte valor aproximado

Resposta

Exercícios de Livros Relacionados

De uma amostra aleatória de domicílios, listamos o número de aparelhos de televisão. Encontre a média e o desvio padrão amostral dos dados.Números de televisores 0 1 2 3 4 5Números de domicílios 1 8 1

Nos exercícios 29 e 30, use a Regra Empírica.O valor médio da TV via satélite de uma amostra de domicílios era de $70,00 por mês com desvio padrão de $14,50 por mês. Entre quais dois valores encontram

De uma amostra aleatória de aviões, listamos o número de defeitos encontrados em suas fuselagens. Encontre a média e o desvio padrão amostrais dos dados.Números de defeitos 0 1 2 3 4 5 6Números de avi

Nos exercícios 27 e 28, encontre a amplitude, a média, a variância e o desvio padrão da amostra.Os salários (em dólares) de uma amostra aleatória de professores do ensino médio.49.632 54.619 58.298 48

Nos exercícios 37 a 40, use o conjunto de dados, que representa a economia de combustível (em milhas na rodovia por galão) de diversas motos Harley-Davidson. (Fonte: Total Motorcycle).53 57 60 57 54 5